SOLUTION: x+4÷x-2<2÷x+1

Algebra ->  Inequalities -> SOLUTION: x+4÷x-2<2÷x+1      Log On


   

Question 981360: x+4÷x-2<2÷x+1
Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
If you mean the way you wrote it, then

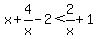
x%2B4%2Fx-2%3C2%2Fx%2B1

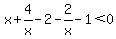
x%2B4%2Fx-2-2%2Fx-1%3C0

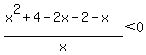
%28x%5E2%2B4-2x-2-x%29%2Fx%3C0

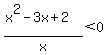
%28x%5E2-3x%2B2%29%2Fx%3C0

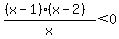
%28%28x-1%29%28x-2%29%29%2Fx%3C0
The two zeros and the undefined x value give three critical values which form the x-number line into four intervals:
The critical values are 0, 1, 2.
The intervals on the x-axis are (-infinity,0), (0,1), (1,2), (2, infinity).

Test any value in each of the intervals and find if it satisfies or not, the inequality.


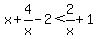
x%2B4%2Fx-2%3C2%2Fx%2B1
Trying x=-1,
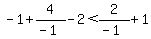
-1%2B4%2F%28-1%29-2%3C2%2F%28-1%29%2B1
-1-4-2%3C-2%2B1
-7%3C-1
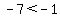
TRUE for (-infinity,0).

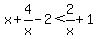
x%2B4%2Fx-2%3C2%2Fx%2B1
Try 1%2F2,
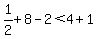
1%2F2%2B8-2%3C4%2B1
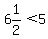
6%261%2F2%3C5
FALSE for (0,1).

Try 3%2F2,
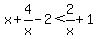
x%2B4%2Fx-2%3C2%2Fx%2B1
3%2F2%2B2%2A4%2F3-2%3C3%2B1
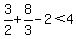
3%2F2%2B8%2F3-2%3C4
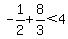
-1%2F2%2B8%2F3%3C4
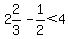
2%262%2F3-1%2F2%3C4
TRUE for (1,2).

Try 4,
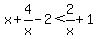
x%2B4%2Fx-2%3C2%2Fx%2B1
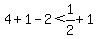
4%2B1-2%3C1%2F2%2B1
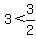
3%3C3%2F2
FALSE for (2, infinity)

This is not yet completely solved. The value for x at 0 cannot be used or included, but the roots of the numerator in the single expression mean that x at 1 and x at 2 SHOULD still be checked, just to be sure of any more thorough solution.

You could try that...