Question 981217: Good day, can you help me solve this problem?
Determine the value of β that will satisfy the ff.
sin (5β-10°) = 1/sec(3β+4°)
Thank you!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  <---> <--->
Applying that,
 ---> --->
The expressions on both sides of the equal sign must be both positive, or both negative.
If they are both positive,
the angles measuring  and and 
are both in quadrant I.
For two angles between  and and  , ,
if the sine of an angle and the cosine of the other are the same,
the angles are complementary (their measures add to  ). ).
In that case, we would have
 ---> ---> ---> ---> ---> ---> ---> ---> . .
(That makes  and and  ). ).
However, since coterminal angles have the same trigonometric function values,
there are other solutions with both angles in the first quadrant,
but their measures adding to 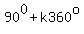 , with , with  = any integer. = any integer.
 ---> ---> ---> ---> ---> ---> ---> ---> for any for any  integer. integer.
So, 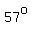 , ,  , , 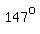 , , 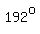 , etc are solutions, , etc are solutions,
and so are 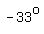 , ,  , , 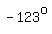 , , 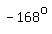 , etc. , etc.
If 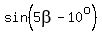 and and 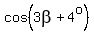 are both negative, are both negative,
the angles measuring  and and 
are both in quadrant III.
They could be both be between  and and 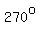 , ,
measuring  more than their quadrant I reference angles, more than their quadrant I reference angles,
and in that case their measures would add up to
 . .
one or both could be coterminal with angles measuring between  and and 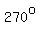 , ,
and in that case their measures would add up to

In either case, the equation and solution would be the same as above:
 and and  for any for any  integer. integer.
|
|
|