Question 981057: x^2/9+(y+3)^2/25=1
whats its center, length of major axis, length of minor axis,foci, and vetexes?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!  .....if you compare it to the standard formula of an ellipse , .....if you compare it to the standard formula of an ellipse , , you see that: , you see that:


so, the center is at ( , , ) )
you also see that we have vertical major axis
 => => and and 
 => => and and 
so,
semi-major axis length is 
semi-minor axis length is
find foci:
first we need 



 and and 
so, foci will be at ( , ,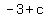 ) and ( ) and ( , ,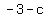 ) )
( , , 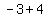 ) => ( ) => ( , ,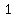 ) )
and
( , , 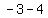 ) => ( ) => ( , , ) )
The vertices are at the intersection of the major axis and the ellipse.
vertices are at ( , ,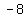 ) and ( ) and ( , , ) )
eccentricity 

|
|
|