Question 981021: Please help me with this problem: given the distance between (x,1) and (-2,5) is 2 sqrt (7) find the value of x.
Found 2 solutions by Fombitz, MathLover1:
Answer by Fombitz(32388)   (Show Source):
Answer by MathLover1(20850)  (Show Source):
You can put this solution on YOUR website! The first point is ( , ). The second point is ( , ).
Since the first point is ( , ), we can say (,) = (,)
So  , 
Since the second point is ( , ), we can also say (,) = (,)
So  ,  .
Now use the distance formula:
since given  , ,,, and , substitute these values
 .......square both sides
 ...........use quadratic formula
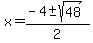
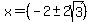
solutions:
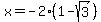
or
so, the first point is (,) could be:
( ,)
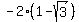or
( ,)
|
|
|
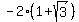