SOLUTION: 1. Four trumpet players' instruments are mixed up, and the trumpets are given to the players just before a concert. What is the probability that no one gets his or her trumpet ba

Algebra ->  Test -> SOLUTION: 1. Four trumpet players' instruments are mixed up, and the trumpets are given to the players just before a concert. What is the probability that no one gets his or her trumpet ba      Log On


   

Question 980989: 1. Four trumpet players' instruments are mixed up, and the trumpets are given to the players just before a concert. What is the probability that no one gets his or her trumpet back?
Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
Given n things in a certain order, the number of "derangements" or 
ways to rearrange them so that none of them are in the same position
they were in before rearranging is given by the formula !n, known as 
n-subfactorial.

The formula for !n is 

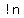
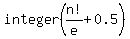%22%21n%22%22%22=%22%22integer%28n%21%2Fe%2B0.5%29

So the number of ways no trumpet player gets his or her own trumpet back is

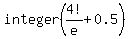
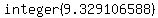
%22%214%22%22%22=%22%22integer%284%21%2Fe%2B0.5%29%22=%22%22integer%2824%2F2.718281828%2B0.5%29%29%22%22=%22%22integer%288.829106588%2B0.5%29%22%22=%22%22integer%289.329106588%29%22%22=%22%229

[Incidentally, FYI, those 9 rearrangements of 

1,2,3,4 are

2,1,4,3
2,3,4,1
2,4,1,3
3,1,4,2
3,4,1,2
3,4,2,1
4,1,2,3
4,3,1,2
4,3,2,1]

The total number of arrangements is 4! = 24.

So the desired probability is 9 ways out of 24.

That's 9/24

Edwin