SOLUTION: 1/2 radical 20 plus radical 45 4 radical 18 minus 3/4 radical 32 minus 1/2 radical 8 radical 20 minus 10 radical 1/5 Please tell me the steps to solve these

Algebra ->  Radicals -> SOLUTION: 1/2 radical 20 plus radical 45 4 radical 18 minus 3/4 radical 32 minus 1/2 radical 8 radical 20 minus 10 radical 1/5 Please tell me the steps to solve these      Log On


   

Question 980823: 1/2 radical 20 plus radical 45
4 radical 18 minus 3/4 radical 32 minus 1/2 radical 8
radical 20 minus 10 radical 1/5
Please tell me the steps to solve these
Answer by josh_jordan(263) About Me  (Show Source):
You can put this solution on YOUR website!
1. 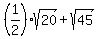%281%2F2%29sqrt%2820%29%2Bsqrt%2845%29

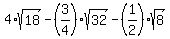
2. 4%2Asqrt%2818%29-%283%2F4%29sqrt%2832%29-%281%2F2%29sqrt%288%29

3. sqrt%2820%29-10%2Asqrt%281%2F5%29

Remember that in order to add and subtract radicals, the numbers inside the radicals must be the same.

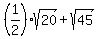
1. %281%2F2%29sqrt%2820%29%2Bsqrt%2845%29

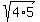In order to add these, we need to reduce each number inside the radicals. So, we need to ask ourselves if there are any numbers, when multiplied together, not only give us the number inside the radicals, but are perfect squares. So, for sqrt%2820%29, we can multiply 4 and 5 together to give us 20, and 4 is a perfect square, because the same number (2) can be multiplied by itself to give us 4: sqrt%284%2A5%29. 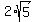The sqrt%284%29 is 2, so we are left with: 2%2Asqrt%285%29. We can multiply 2 by (1/2), which is 1. So %281%2F2%29sqrt%2820%29 can be reduced to sqrt%285%29.

Now let's work on sqrt%2845%29. What two numbers can be multiplied by 45, if one of those numbers is a perfect square? 9 and 5, because 9 is a perfect square (3 x 3 = 9): sqrt%289%2A5%29, which can be reduced to 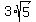3%2Asqrt%285%29. We are left with two terms, both of which have the same number inside the radicals:

sqrt%285%29%2B3%2Asqrt%285%29

We can now add these together:

sqrt%285%29%2B3%2Asqrt%285%29=4%2Asqrt%285%29

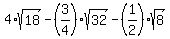
2. 4%2Asqrt%2818%29-%283%2F4%29sqrt%2832%29-%281%2F2%29sqrt%288%29

We will use the same techniques for this question that we used for Question 1:

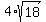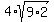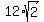
4%2Asqrt%2818%29 -----> 4%2Asqrt%289%2A2%29 -----> %283%29%284%29%2Asqrt%282%29 -----> 12%2Asqrt%282%29

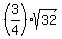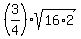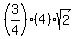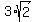
%283%2F4%29sqrt%2832%29 -----> %283%2F4%29sqrt%2816%2A2%29 -----> %283%2F4%29%284%29%2Asqrt%282%29 -----> 3%2Asqrt%282%29

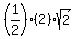%281%2F2%29sqrt%288%29 -----> %281%2F2%29sqrt%284%2A2%29 -----> %281%2F2%29%282%29%2Asqrt%282%29 -----> sqrt%282%29

Now we can perform the operation:

12%2Asqrt%282%29-3%2Asqrt%282%29-sqrt%282%29 -----> 8%2Asqrt%282%29

3. sqrt%2820%29-10%2Asqrt%281%2F5%29

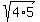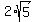
sqrt%2820%29 -----> sqrt%284%2A5%29 -----> 2%2Asqrt%285%29

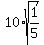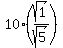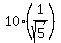
10%2Asqrt%281%2F5%29 -----> 10%2A%28sqrt%281%29%2Fsqrt%285%29%29 -----> 10%2A%281%2Fsqrt%285%29%29

We know have to rationalize our denominator sqrt%285%29 since we cannot have a square root in the denominator. To do this, we will multiply both the numerator and denominator by sqrt%285%29:

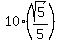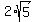
10%2A%28%281%2Asqrt%285%29%29%2F%28sqrt%285%29%2Asqrt%285%29%29%29 -----> 10%2A%28sqrt%285%29%2F5%29 -----> 2%2Asqrt%285%29

We can now perform the indicated operation:

2%2Asqrt%285%29-2%2Asqrt%285%29=0