Question 980545: An open-top, square bottom crate is made of two materials--the sides are made of a light material that costs $3 per square foot and the bottom is made with a heavier material that costs $5 per square foot. If the volume of the crate has to be 5 cubic feet, what should be the dimensions of the crate to minimize the cost of the materials to build the crate. Assume that the labor and assembly materials cost the same no matter the dimensions of the crate and excess materials can be reused.
The available multiple choice answers for my homework problem are:
1) Base is 2ft x 2ft and Height is 1.25ft
2) Base is 1.82ft x 1.82ft and Height is 1.51ft
3) Base is 2.24ft x 2.24ft and Height is 1ft
4) Base is 5ft x 1ft and Height is 1ft
Thanks.
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
You can put this solution on YOUR website! x, base dimensions
y, how tall
Bottom Material, $5 per sq ft
Sides Material, $3 per sq ft
Volume must be 5 cubic feet
A, for area of surfaces (outer or inner, but not both);
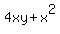 . .
Let c be cost of the box.


Volume of 5 feet^3,


Use this in the cost equation:


CALCULUS PROCESS TO FIND x FOR MINIMUM COST
Find dc/dx, set equal to 0, solve and examine any or all solutions which occur; one of them should correspond to the x for minimum cost. Once found x, use it to evaluate y. Note, I did not finish this but only described it. You could probably do with no trouble.
-
If you do not yet know derivative from Calculus, then maybe just use a graphing calculator or other graph software.
|
|
|