Question 980441: The load that can supported by a rectangular beam varies jointly as the width of the beam and the square of its height, and inversely as the length of the beam. A beam 12 feet long, with a width of 6 inches and a height of 4 inches can support a maxiumum load of 800 pounds. If a similar board has a width of 9 inches and a height of 5 inches, how long must it be to support 1,200 pounds?
Found 2 solutions by onlinepsa, ikleyn:
Answer by onlinepsa(22)   (Show Source): (Show Source):
You can put this solution on YOUR website! Load supported can be expressed as,
L= k* (h^2) * w / l
In first case:
800 = k* (4^2) * 6/144
k= 1200
In the second case:
1200 = 1200* (5^2) * 9/l
=> l = 25 * 9 = 225 inch = 18.7 feet approx.
Thanks,
PRD
https://onlinepsa.wordpress.com/
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The condition of this problem means exactly the following:
The load that can be supported by a rectangular beam is proportional to the width of the beam multiplied by the square of its height
and divided by the length of the beam.
In other words,
 = =  . .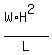 , ,
where  is the critical load, is the critical load,  is the width of the beam, is the width of the beam, 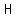 is its height, is its height,  is the length of the beam and is the length of the beam and  is the proportionality coefficient which is the constant value for the selected unit system. is the proportionality coefficient which is the constant value for the selected unit system.
It is how this English is translated to Algebra.
Therefore, to estimate the critical load, you need to calculate the value of 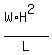 for each set of data. for each set of data.
For the first set you have
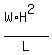 = = 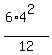 = = 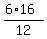 = =  . .
For the second set you have
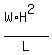 = = 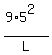 = = 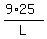 = = 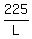 . .
Now, you have the proportion to find the required L:
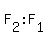 = = 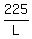 : :  . .
Substitute here the given critical loads and solve the proportion (the equation) for the unknown L step by step:
 = =  , ,
 = =  , ,
3*8*L = 2*225,
L =  = =  = 20.833 ft. = 20.833 ft.
Answer. The beam with the width of 9 inches and height of 5 inches must be no longer than 20.833 ft to be able to support the load of 1200 pounds.
Couple of notes
1. The formulation of the problem must start with these words:
"The load that can be supported by a rectangular beam . . . "
instead of
"The load that can supported by a rectangular beam . . . "
2. It doesn't matter in this problem that different dimensions (width, height and length) are presented in different units (feet and inches).
What is really important in this context that the corresponding dimensions must be presented in the same units (length and length, width and width, height and height).
Otherwise you are obliged to make the conversion of dimensions.
|
|
|