Question 980343: x^2/25+y^2/16=1
what are its vertices,foci,eccentricty of the ellipse?
length of major and minor axis?
Answer by ikleyn(52810)   (Show Source): (Show Source):
You can put this solution on YOUR website!
You are given the ellipse
 + + 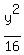 = =  . .
The canonical equation of this ellipse is (see the lesson Ellipse definition, canonical equation, characteristic points and elements in this site)
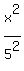 + + 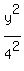 = =  . .
Vertices: (-5, 0); (5, 0); (0, 4); (0, -4).
Length of major axis is 2*5 = 10; (along the x-axis)
Length of minor axis is 2*4 = 8; (along the y-axis)
Linear eccentricity: c = 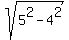 = = 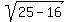 = =  = 3. = 3.
Eccentricity: 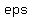 = =  = =  = 0.6. = 0.6.
Foci: (-c, 0) = (-3, 0) and (c, 0) = (3, 0)
(Foci lie in the x-axis)
|
|
|