Question 980173: There was a question about an army travelling 5 mph and a messenger on horseback travelling at 10 mph(question asks for the distance from front to rear) that was answered by ankor@dixie.net that I didn't really understand why did he add and subtract 5 to the 10 mph rate. I know that you do add +-r or a given amount in wind and water current problems. Is that why you added and subtracted the 5? Some logic of why is all I need, so that I can understand a problem that I've never seen before in any other place than the Schaum College Algebra textbook. Please help. QUESTION: WHY WAS THE 5 ADDED AND SUBTRACTED FROM 10 TO GET 15 AND 5(Denominators) AND WHY 5 AND NOT R? Anybody that understands fully why and can explain is welcome.
Found 3 solutions by josmiceli, josgarithmetic, ikleyn:
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! The moving army is the exact opposite of the
current in a stream because the motion of the
army has ZERO effect on the messenger's
motion.
If you are moving in the same direction as the army
at 10 mi/hr and the army is moving at 1 mi/hr
you can imagine the army is stopped and you are
moving at  mi/hr mi/hr
If the army was a stream moving in the same
direction, the current would ADD to the
messenger's motion
--------------------------------
If you are moving opposite to the direction of the army,
imagine that the army is stopped, and you are moving
at the sum = 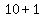 mi/hr mi/hr
------------------------------
Just think about the current of a stream having a direct
effect on a boat ( adding or subtracting )
Think about the army as the background against which
you are moving either whizzing by you making it easy
to get where you are going, or the background is moving
away from you making it harder to get where you're going
Hope this helps
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Add or Subtract depends which way or direction the student uses as positive or negative. Travel rate is a vector; speed is just the size of the vector quantity. The group is going in a direct, and the messenger, starting from the front of the group, brings a traveling message IN THE OPPOSITE DIRECTION than the group is traveling. Accordingly, the signs of the group and of the messenger are opposite.
Answer by ikleyn(52782)   (Show Source): (Show Source):
|
|
|