SOLUTION: Find the discontinuiny, and the zeros of the function for f(x) = the quantity negative x squared plus x plus 20 over the quantity x plus 4 (-x^2+x+20/x+4)

Algebra ->  College  -> Linear Algebra -> SOLUTION: Find the discontinuiny, and the zeros of the function for f(x) = the quantity negative x squared plus x plus 20 over the quantity x plus 4 (-x^2+x+20/x+4)      Log On


   

Question 980068: Find the discontinuiny, and the zeros of the function for f(x) = the quantity negative x squared plus x plus 20 over the quantity x plus 4 (-x^2+x+20/x+4)
Answer by josh_jordan(263) About Me  (Show Source):
You can put this solution on YOUR website!
To find the discontinuity of the function 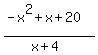%28-x%5E2%2Bx%2B20%29%2F%28x%2B4%29 we will look at the denominator and determine what value for x will result in the denominator equalling 0, since the denominator cannot equal 0. To do this, we will set our denominator equal to 0:

x + 4 = 0

Subtract 4 from both sides, giving us:

x = -4

Therefore, our discontinuity is x = -4

To find our zeroes, we will set our function equal to 0:

%28-x%5E2%2Bx%2B20%29%2F%28x%2B4%29=0

Next, multiply both sides of the equation by (x + 4) to rid ourselves of our fraction on the left side of the equal sign. This will result in:

-x%5E2%2Bx%2B20=0

Third, multiply the entire equation by -1 to make the equation easier to factor. This will give us:

x%5E2-x-20=0

Fourth, factor the left side of the equation. This will result in:

%28x-5%29%28x%2B4%29=0

Set each set of parentheses equal to zero and solve for x:

%28x-5%29=0 -----> x=5

%28x%2B4%29=0 -----> x=-4

Since we have determined that -4 is NOT a zero since it will result in a zero value in our denominator, our only zero is x=5

We can verify by substituting the x in our original equation with 5:

%28-%285%5E2%29%2B%28-5%29%2B20%29%2F%285%2B4%29=0 -----> %28-25-5%2B20%29%2F9=0 -----> 0%2F9=0 -----> 0=0.

Since 0=0 is a true statement, 5 is, in fact, the zero of our function.