|
Question 980041: The product of two consecutive odd integers is 1 less than 5 times their sum. Find the two integers. Answer in the form of paired points with the lowest of the two integers first.
Answer by josh_jordan(263)   (Show Source):
You can put this solution on YOUR website! To solve, let's first find a way to represent the first integer and the second integer. We'll use the letter a:
Integer 1: a
Integer 2: a + 2 (because 2 more than our first odd number will be the next consecutive odd number)
Next, let's convert our word problem into an equation.
"The product of two consecutive odd integers": (a)(a + 2) or a x (a+2)
"is": =
"1 less than 5 times their sum": 5(a + a + 2) - 1
Now, let's put it all together: (a)(a + 2) = 5(a + a + 2) - 1, which is the equation we will use.
To solve for a (which is our first odd integer), first let's simplify each side of our equal sign:
(a)(a + 2) -----> 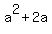 and 5 (a + a + 2) - 1 -----> 5(2a + 2) - 1 -----> 10a + 10 - 1 -----> 10a + 9. So, now we have:
Next, move everything on the right side of the equation to the left side of the equation and combine all like terms on the left side of the equation:
 -----> 
Our next step is to factor , which will give us:
(a - 9)(a + 1) = 0
Set each set of parentheses equal to 0 to solve for a, which will give us two different values for a:
a - 9 = 0 -----> a = 9
a + 1 = 0 -----> a = -1
We now know that our first odd integer is both 9 and -1. To find both of our second pair of odd integers, we will replace a in a + 2 with both 9 and -1:
a + 2 ----> 9 + 2 -----> 11
a + 2 -----> -1 + 2 -----> 1
So, when our first integer is 9, the next consecutive odd integer is 11, and when our first integer is -1, the next consecutive odd integer is 1. In paired point form, with the lowest of the two integers first, our answer would be:
(-1, 1) and (9, 11)
|
|
|
| |
