SOLUTION: If {{{ x = sqrt( pq ) }}} and {{{ y = expr(1/2) (p+q) }}} prove that x < y

Note:  It must be stated that 

p ≧ 0, q ≧ 0, pq > 0, p ≠ q, 

otherwise the inequality is false.  I'll assume these,
but first I'll give two examples to show you that this 
is false without those assumptions.

It isn't true when p=-8, q=-2 because




Yet 4 < -5 is false.

It also isn't true when p=1, q=1 because




Yet 1 < 1 is false.

It must be stated that p ≧ 0, q ≧ 0, pq > 0, p ≠ q,

It is also easy to see that it is true if p is 0 and q isn't 
or if q is 0 and p isn't, but they both cannot be 0.

-------------------------------------------
Here is the proof

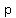  assumed as given



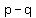The square of any non-zero number is positive, so
we can square both sides:





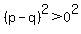
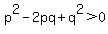add 4pq to both sides:



Factor the left side



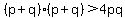Write left side as the square of a binomial:



Take non-negative square roots of both sides 





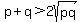Multiply both sides by 1/2:





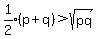
Same as 



Edwin