SOLUTION: The cost C of a pound of a margarine in 2006 was 66 cents. in 2010 the cost was 83 cents. assuming the exponential growth model applies: A: Find the exponential growth rate to t

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: The cost C of a pound of a margarine in 2006 was 66 cents. in 2010 the cost was 83 cents. assuming the exponential growth model applies: A: Find the exponential growth rate to t      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 979663: The cost C of a pound of a margarine in 2006 was 66 cents. in 2010 the cost was 83 cents. assuming the exponential growth model applies:
A: Find the exponential growth rate to the nearest tenth of a percent, and write the equation.
B: Find the cost of a pound of margarine in 2012 and 2018
Answer by josgarithmetic(39625) About Me  (Show Source):
You can put this solution on YOUR website!
You may have a choice of C=pb%5Ex or C=pe%5E%28kx%29. You can use any base b you want, which may be 10, or 2, or e, and the initial cost for a pound is the variable p. e is the base of the Natural Logarithm, for the second choice of equation model, which will involve a constant k as part of the exponent.


Which form of the model? Your choice.

This help posting will use the first one.
EITHER base you like, find logarithm of both sides. I will use natural log base just for convenience. You use base ten, if you want.


ln%28C%29=ln%28pb%5Ex%29
ln%28C%29=ln%28p%29%2Bln%28b%5Ex%29
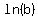ln%28C%29=ln%28p%29%2Bx%2Aln%28b%29
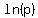highlight_green%28ln%28C%29=ln%28b%29%2Ax%2Bln%28p%29%29-------This is a linear equation having slope ln%28b%29 and vertical axis intercept ln%28p%29.

The points to use for this linear form need to use natural log of the costs, because the linear equation defines a formula for the natural log of cost.

The ordered pairs for your points are (2006, ln(66)) and (2010, ln(83)).

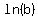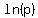You already have learned what to do with a system of two linear equations. Using each pair of points gives a corresponding equation, and the new unknowns to solve for will be ln%28b%29 for slope and ln%28p%29 for vertical axis intercept.