|
Question 979565: A,B can do a piece of work 6,8 hours respectively.If they work for a day alternatively.Suppose A beginning the work,in how many days work will be completed?
i think answer is 6 ³/2.
please explain this question.
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website! Your description might be better understood as, "A and B working independently and not at the same time on the same job, take 6 and 8 hours respectively". They can still work "ALTERNATELY" on a task.
WORKER________RATE, job/hours
A_____________1/6
B_____________1/8
Now, the rest of the description gives A and B working in alternation. Each is working on the job separately, not simultaneously. We could try making calculation at a very low level.
(1/6)*1+(1/8)*1+(1/6)*1+(1/8)*1+....=1
Try maybe using a variable for the number of day that EACH may possibly work alone, although the true result could be non-whole.
Say like, A and B each works x days.
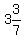 , which is  days.
Try to now go back to the lowest day to day level.
First let A work for 3 days and B work for 3 days, knowing that A and B never work on the same day.
-
This way, three days for A and three days for B, done in alternation,
completes only  of the job, and the work began with worker A. B worked last, so A does ONE MORE day...
-
This then is slightly MORE THAN 1 JOB.
Let me just summarize as much as to say, A will work for 4 days, and then B will have worked 3 days, plus most of the last day but not all of it.
|
|
|
| |
