Question 979561: x^4-3x^3+2x^2/x^2-x-30>=0
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Here is a start:
Is the quadratic factor of numerator factorable?
The discriminant,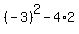 
-
roots  and 
or
roots 1 and 2
-
That quadratic factor is further factorable as  .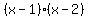
The entire inequality is  .
You want to check the intervals cut by the critical x values of -5, 0, 1, 2, 6.
Some intervals will satisfy and others will not satisfy the given inequality.
-
Check any single value in these intervals of x:
(-infinity,-5), (-5,0], [0,1], [1,2], [2,6), (6,infinity).
|
|
|
