|
Question 978968: Here is the question I'm stuck on:
Give an equation of each line described:
a) Through the point (2,5) with slope -3/4
b) through the points (3,-1) and (0,6)
c) horizontal line through (-2,-7)
d) line through the point (6,5) and parallel to the line 2x + 3y = 7
e) line through the point (4,1) and perpendicular to the line x + 5y = 1
That is all. Thank you so much for taking time out of your day to help me!
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) Through the point ( , , ) with slope ) with slope 

if slope  , we have , we have

now use given point ( , , )=( )=( , , ) and find ) and find 






so, your equation is 

b) through the points ( , , ) and ( ) and ( , , ) )
| Solved by pluggable solver: Find the equation of line going through points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (3, -1) and (x2, y2) = (0, 6).
Slope a is  . .
Intercept is found from equation  , or , or  . From that, . From that,
intercept b is  , or , or  . .
y=(-2.33333333333333)x + (6)
Your graph:

|
c) horizontal line through ( , , ) )
For a horizontal line equation will be  where where  is a constant. is a constant.
For the line to pass through the point ( , , ) )  should be equal to should be equal to  . .
Your line should be


d) line through the point ( , , ) and parallel to the line ) and parallel to the line 


| Solved by pluggable solver: Finding the Equation of a Line Parallel or Perpendicular to a Given Line |
Since any two parallel lines have the same slope we know the slope of the unknown line is 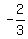 (its from the slope of (its from the slope of  which is also which is also 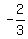 ).
Also since the unknown line goes through (6,5), we can find the equation by plugging in this info into the point-slope formula ).
Also since the unknown line goes through (6,5), we can find the equation by plugging in this info into the point-slope formula
Point-Slope Formula:
 where m is the slope and ( where m is the slope and ( , ,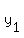 ) is the given point ) is the given point
 Plug in Plug in  , ,  , and , and 
 Distribute Distribute 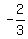
 Multiply Multiply
 Add Add  to both sides to isolate y to both sides to isolate y
 Make into equivalent fractions with equal denominators Make into equivalent fractions with equal denominators
 Combine the fractions Combine the fractions
 Reduce any fractions Reduce any fractions
So the equation of the line that is parallel to  and goes through ( and goes through ( , , ) is ) is 
So here are the graphs of the equations  and and 
 graph of the given equation graph of the given equation  (red) and graph of the line (red) and graph of the line  (green) that is parallel to the given graph and goes through ( (green) that is parallel to the given graph and goes through ( , , ) )
|
e) line through the point ( , , ) and perpendicular to the line ) and perpendicular to the line 


| Solved by pluggable solver: Finding the Equation of a Line Parallel or Perpendicular to a Given Line |
Remember, any two perpendicular lines are negative reciprocals of each other. So if you're given the slope of  , you can find the perpendicular slope by this formula: , you can find the perpendicular slope by this formula:
 where where 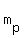 is the perpendicular slope is the perpendicular slope
 So plug in the given slope to find the perpendicular slope So plug in the given slope to find the perpendicular slope
 When you divide fractions, you multiply the first fraction (which is really When you divide fractions, you multiply the first fraction (which is really  ) by the reciprocal of the second ) by the reciprocal of the second
 Multiply the fractions. Multiply the fractions.
So the perpendicular slope is 
So now we know the slope of the unknown line is  (its the negative reciprocal of (its the negative reciprocal of  from the line from the line  ).
Also since the unknown line goes through (4,1), we can find the equation by plugging in this info into the point-slope formula ).
Also since the unknown line goes through (4,1), we can find the equation by plugging in this info into the point-slope formula
Point-Slope Formula:
 where m is the slope and ( where m is the slope and ( , ,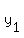 ) is the given point ) is the given point
 Plug in Plug in  , ,  , and , and 
 Distribute Distribute 
 Multiply Multiply
 Add Add  to both sides to isolate y to both sides to isolate y
 Combine like terms Combine like terms
So the equation of the line that is perpendicular to  and goes through ( and goes through ( , , ) is ) is 
So here are the graphs of the equations  and and 
 graph of the given equation graph of the given equation  (red) and graph of the line (red) and graph of the line  (green) that is perpendicular to the given graph and goes through ( (green) that is perpendicular to the given graph and goes through ( , , ) )
|
|
|
|
| |