SOLUTION: We are to find the value of {{{x^4+x^4+z^4}}} when X, Y and Z are real numbers which satisfy the following three equalities: {{{x+y+z=3}}} {{{x^2+y^2+z^2=9}}} {{{xyz= -2}}}

Algebra ->  Expressions-with-variables -> SOLUTION: We are to find the value of {{{x^4+x^4+z^4}}} when X, Y and Z are real numbers which satisfy the following three equalities: {{{x+y+z=3}}} {{{x^2+y^2+z^2=9}}} {{{xyz= -2}}}       Log On


   

Question 978785: We are to find the value of 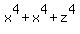x%5E4%2Bx%5E4%2Bz%5E4 when X, Y and Z are real numbers which satisfy the following three equalities:
x%2By%2Bz=3
x%5E2%2By%5E2%2Bz%5E2=9
xyz=+-2
Firstly, it follows from the first two equalities that
xy%2Byz%2Bzx+=+A
Next using

we have
x%5E4%2By%5E4%2Bz%5E4=C
Answer by richwmiller(17219) About Me  (Show Source):
You can put this solution on YOUR website!
x+y+z=3,
x^2+y^2+z^2=9,
xyz= -2,
x^4+x^4+z^4=c
c = 57-32 sqrt(3), x = 1-sqrt(3), y = 1+sqrt(3), z = 1
c = 57+32 sqrt(3), x = 1-sqrt(3), y = 1+sqrt(3), z = 1
c = 84+16 sqrt(3), x = 1-sqrt(3), y = 1, z = 1+sqrt(3)
c = 84-16 sqrt(3), x = 1-sqrt(3), y = 1, z = 1+sqrt(3)
c = 30-16 sqrt(3), x = 1, y = 1-sqrt(3), z = 1+sqrt(3)
c = 30+16 sqrt(3), x = 1, y = 1-sqrt(3), z = 1+sqrt(3)