SOLUTION: So far a total of 48 tickets have been sold for the school play for a total revenue of $220. How many student tickets have been sold? Set up and solve a system of equations to solv

Algebra ->  Coordinate Systems and Linear Equations  -> Linear Equations and Systems Word Problems -> SOLUTION: So far a total of 48 tickets have been sold for the school play for a total revenue of $220. How many student tickets have been sold? Set up and solve a system of equations to solv      Log On


   

Question 978484: So far a total of 48 tickets have been sold for the school play for a total revenue of $220. How many student tickets have been sold? Set up and solve a system of equations to solve the problem.
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
You forgot to tell us how much the tickets cost each.
So I just arbitrarily chose that the price of a student 
ticket is $4 and the price of a non-student ticket is $6. 


Let the number of student tickets be x
Let the number of non-student tickets be y

                      Price     Money
 Type      Number      of        from
  of        of        EACH       ALL
ticket    tickets     ticket   tickets
-------------------------------------------
student      x         $4       $4x
non-student  y         $6       $6y
-------------------------------------------
TOTALS      48       -----     $220

 The first equation comes from the second column.

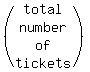  %28matrix%284%2C1%2CNumber%2Cof%2Cstudent%2Ctickets%29%29%22%22%2B%22%22%28matrix%284%2C1%2CNumber%2Cof%2Cnon-students%2C+tickets%29%29%22%22=%22%22%28matrix%284%2C1%2Ctotal%2Cnumber%2Cof%2Ctickets%29%29
               x + y = 48

The second equation comes from the last column:

  %28matrix%285%2C1%2CMoney%2Cfrom%2CALL%2Cstudent%2Ctickets%29%29%22%22%2B%22%22%28matrix%285%2C1%2CMoney%2Cfrom%2CALL%2Cnon-student%2Ctickets%29%29%22%22=%22%22%28matrix%285%2C1%2CTotal%2Cmoney%2Cfrom%2CALL%2Ctickets%29%29

             4x + 6y = 220

So we have this system of equations:

system%28x+%2B+y+=+48%2C4x+%2B+6y+=+220%29.

We solve by substitution.  Solve the first equation for y:

               x + y = 48
                   y = 48 - x

Substitute (48 - x) for y in 4x + 6y = 220

   4x + 6(48 - x) = 220
    4x + 288 - 6x = 220
        -2x + 288 = 220
              -2x = -68
                x = 34 = the number of student tickets.

Substitute in y = 48 - x
              y = 48 - (34)
              y = 14 non-student tickets.

Checking:  34 student tickets brings in $136 and 14 non-students is $84
            That's 48 tickets.
            And indeed $136 + $84 = $220

Edwin