Question 978179: My age this year is a multiple of 8.Next year it will be a multiple of 7.How old am i?
Found 2 solutions by Edwin McCravy, KMST:
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website! My age this year is a multiple of 8.Next year it will be a multiple of 7.How old
am i?
List the multiples of 8 up to an age than nobody lives to.
8,16,24,32,40,48,56,64,72,80,88,96,104,112,120
List the multiples of 7 up to an age than nobody lives to.
7,14,21,28,35,42,49,56,63,70,77,84,91,98,105,112,119
Look through the lists to find one in each list such that the one
in the second list is 1 more than the one in the first list.
We find 48 in the first list and 49 in the second list.
We find 104 in the first list and 105 in the second list.
(Many people have lived to be 104, and there are some living now that old!).
Two solutions. "I am 48" or "I am 104"
Edwin
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! TRIAL AND ERROR:
the current age is a multiple of 8, so we try different multiples of 8.
We can make a table with reasonable ages that are multiples of 8,
and see if the age next year (age+1) would be a multiple of 7.
The age of that person should be  this year, and will be 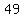 at some time next year.
A person could be 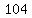 and expect to have another birthday next year,
but it is very rare to be that old,
and someone that old would probably not be asking math question like that one.
MAKING IT LOOK MORE LIKE ALGEBRA:
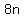 = age this year (for some number  that is a positive integer).
 = age next year (for some number  that is a positive integer).
Let us get some useful relationship from that:
We know that  is a positive integer, so 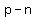 must be a positive integer too.
 gives us  ---> ---> and since  ,
 ---> --->
 gives us  ---> ---> and since ,
 ---> ---> ,
which not a very reasonable answer, as it is unlikely to reach age 104
while expecting to live until the next year and the next birthday,
and asking this kind of math question.
However, if I am in good physical and mental health 40 years from now,
I will post the same question and cackle with glee.
FOR A TRICK QUESTION
I do not think it is meant to be a trick question, so I would answer the answer above.
For a trick question,
that person could have had a birthday and turned  earlier this yea.
So, at the beginning of next year would still be (until the next birthday.
As  is a multiple of  and a multiple of ,
that person's age would be = a multiple of now,
and = a multiple of  for some time next year,
at the beginning of the year, before the next birthday,
|
|
|
