Question 978130: Write the complex number 6 + 8i in trigonometric form.
A.
10(cos 306.9° + i sin 306.9°)
B.
10(cos 233.1° + i sin 233.1°)
C.
10(cos 53.1° + i sin 53.1°)
D.
10(cos 126.9° + i sin 126.9°)
I tried this and got 10(cos(0.92729522)+isin(0.92729522)) ??
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your answer is right, understanding that you are expressing the angle in radians.
Since the multiple choice answers have the angle measured in degrees,
none of the options given looks like a match.
In this case, no calculations are needed to pick the right answer.
Because the real part and the imaginary part of 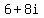 are positive numbers, are positive numbers,
you know that the sine and cosine must be positive,
meaning that the angle must be between  and and  , ,
so the answer is obviously 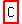 . .
If we had to calculate, we would calculate
 for the modulus, for the modulus,
and we would pick an angle  such that such that

Using a cheap scientific calculator in degree mode, I get that the angle is approximately  , which rounds to , which rounds to 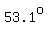 . .
If I had not found that calculator quickly enough,
I would have used Excel that would give me the 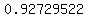 (radian) answer you posted. (radian) answer you posted.
Them, I would have converted to degrees by multiplying times 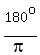 ; ;
 (rounded). (rounded).
|
|
|