Question 97784: Find the vertices and foci of the ellipse given by:
x^2+9y^2-24x+18y+9=0
Answer by mathslover(157)   (Show Source): (Show Source):
You can put this solution on YOUR website! The standard form of the equation of an ellipse is
 where (h,k) is the center of the ellipse where (h,k) is the center of the ellipse
we first try and put the given equation in the standard form







so we have the center (h,k) as (12,-1)
also a=12 and b=4
Since a > b the major axis is horizontal
vertices are given by (h-a,k) and (h+a,k)
so we have ( 12-12,-1) and (12+12,-1)
vertices are (0,-1) and (24,-1)
focii are at points given by (h-c,k) and (h+c,k) where c = 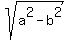
(12- 8*sqrt2,-1) and (12+ 8*sqrt2,-1)
|
|
|