SOLUTION: Hi there tutors, can you help me out answer this question? Thanks Five consecutive positive integers, p, q, r, s and t, each less than 10000, produce a sum which is a perfect sq

We have consecutive positive integers p, q=p+1, r=p+2, s=p+3, t=p+4

p+q+r+s+t = A², where A is some positive integer

p+(p+1)+(p+2)+(p+3)+(p+4) = 5p+10 = A²

5p+10 = A²
5(p+2) = A²
So A is a multiple of 5, say A = 5B where B is a positive integer.
5(p+2) = (5B)²
5(p+2) = 25B²
p+2 = 5B²
p = 5B²-2

q+r+s = C³ where C is a positive integer
(p+1)+(p+2)+(p+3) = C³
3p+6 = C³
3(p+2) = C³
So C is a multiple of C, say C = 3D where D is a positive integer.
3(p+2) = (3D)³
3(p+2) = 27D³
p+2 = 9D³
p = 9D³-2

p = 5B²-2 = 9D³-2

p+2 = 5B² = 9D³

B must be a multiple of 3 to create the 9 factor on the right.
D must be a multiple of 5 to create the 5 factor on the left
Then B must be a multiple of 5 since D³ will produce 3 factors of 5.

So B must be a multiple of 3 and 5, so we take B = 15 and D = 5

p+2 = 5(15)² = 9(5)³
p+2 = 1125 = 1125

That works, so

So p = 1125-2 = 1123

So (p,q,r,s,t) = (1123,1124,1125,1126,1126)

Checking

p+q+r+s+t = 1123+1124+1125+1126+1127 = 5625 = 75²

q+r+s = 3375 = 15³

Answer:  

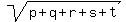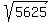Edwin