SOLUTION: p(x)=x^4-2x^3-8x+16 factor the polynomial and use the factored form to find the zeros x=?

p(x) = x⁴-2x³-8x+16

Out of the first two terms on the right, factor out x³

p(x) = x³(x-2)-8x+16

Out of the last two terms on the right, factor out -8,
being careful to remember that when you factor a negative
out of a positive, -8 out of +16, you get a negative inside 
the parentheses:

p(x) = x³(x-2)-8(x-2)

Now there is a common factor of (x-2) in both terms so we
factor (x-2) out of both terms:

p(x) = (x-2)(x³-8)

Now since 8 = 2³, we have

p(x) = (x-2)(x³-2³)

And now we use the rule for factoring the difference of two cubes:

p(x) = (x-2)(x-2)(x²+2x+2²)

p(x) = (x-2)²(x²+2x+4)

The only real zero is found by setting factor x-2 equal 0

x-2 = 0
  x = 2

It has multiplicity 2 because p(x) has two factors (x-2)(x-2) which 
when set = 0, provide the zero 2.

There are also two imaginary zeros which we find by setting the other
factor x²+2x+4 equal to 0 and using the quadratic formula since it
does not factor:

x²+2x+4 = 0
   






















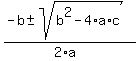
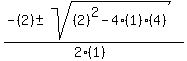
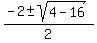
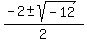
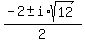
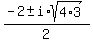
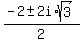
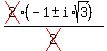
So there are three zeros, 1 real solution of 2 which has multiplicity 2,
and two conjugate imaginary or complex zeros 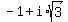 and .

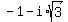Edwin