Question 977183: Hello!
I need help solving this.
f(x)= x^2-3x-18/(x^2-4)
What is the domain of the function, x-intercepts, y-intercept, vertical asymptote and horizontal asymptote and graph.
Please explain each step.
Thank you
Found 2 solutions by Boreal, MathLover1:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! f(x)= x^2-3x-18/(x^2-4)
the denominator cannot be zero, so x^2-4 cannot be 0, and x cannot be 2 or -2.
y-intercept is when x=0, and that is -18/-4 or 4.5
x-interceps found by factoring (x-3)(x+6)/(x-2)(x+2); x= -3 and x=+6 will make the numerator 0 and therefore make y=0.
vertical asymptote is where x= 2 or -2. At that point, the function goes to either + or - infinity.
horizontal asymptote is where as x becomes infinite, the function approaches a certain value. The squares are what drive the function at infinity. x^2 is so much larger than x, that you can ignore anything that isn't a square. The function then becomes x^2/x^2 or 1. y=1 is the horizontal asymptote.
Graphing by hand, I would draw in the asymptotes, the y-intercept is -4.5, the roots are 2 and -2, and you look at values less than -2, between -2 and 2, and greater than -2.
Greater or less than minus 2, and the function approaches the line y=1.
Less than -2, say -1, f(x)=-14/-3 or +4 2/3.
Less than +2, say +1, f(x)=-20/-3 or +6 2/3
At minus 2.0001, for example, the numerator is about 4-6-18=-20. The denominator is 4.0004-4 or 0.0001. Large negative numerator, small positive denominator. The function has a large negative value. At -1.9999, the denominator is small negative, so the value becomes very large. The same occurs at +1.9999 and +2.0001. You know near an asymptote that the function will go to infinity. What you do is look to see what the sign of both the numerator and denominator are. You don't really need to calculate them, just know that the denominator will become very close to zero. The question then becomes, close to from negative side? or close to from positive side?

Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 




since denominator cannot be equal to zero, domain will be all values of  element of element of 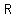 excluding values of excluding values of  that make denominator equal to zero and they are that make denominator equal to zero and they are

if  => =>
if  => =>
so, the domain is
{  element element 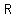 : :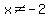 and and  } }
x-intercepts:

if  => =>
if  => =>
x-intercepts are at ( , ,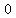 ) and ( ) and ( , ,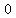 ) )
y-intercepts:if 





y-intercept is at ( , ,  ) )
asymptotes:
since x-intercepts at  and and  , the vertical asymptotes are at , the vertical asymptotes are at  and and 
Other asymptotes, if any, occur for large positive or negative values of x's (way off to the right or left on the graph). To find them you have to analyze the function for high values. One way to do this is to divide the numerator and denominator by the highest power of x in the function. For this equation, that would be  : :
what happens to y for large  's? 's?
When  has very large values, all those little fractions will have very large denominators. And fractions with very large denominators are very small numbers. In fact, the larger has very large values, all those little fractions will have very large denominators. And fractions with very large denominators are very small numbers. In fact, the larger  gets the closer the fraction as a whole gets to gets the closer the fraction as a whole gets to  ! So if we replace replace all those little fractions with an ! So if we replace replace all those little fractions with an  in the denominator with zeros we can see the value that y approaches for large in the denominator with zeros we can see the value that y approaches for large  's: 's:






So  is the horizontal asymptote. is the horizontal asymptote.

|
|
|