SOLUTION: Which of the following is the greatest? a. {{{3^210}}} b. {{{7^140}}} c. {{{17^105}}} d. {{{31^84}}} Please give detailed solution. (NOTE: Don't use logarithm. It has been

Algebra ->  Divisibility and Prime Numbers -> SOLUTION: Which of the following is the greatest? a. {{{3^210}}} b. {{{7^140}}} c. {{{17^105}}} d. {{{31^84}}} Please give detailed solution. (NOTE: Don't use logarithm. It has been       Log On


   

Question 977126: Which of the following is the greatest?
a. 3%5E210
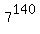
b. 7%5E140
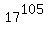
c. 17%5E105
d. 31%5E84
Please give detailed solution.
(NOTE: Don't use logarithm. It has been removed from syllabus, and I have to make my students understand without using log)
Found 2 solutions by Alan3354, solver91311:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Which of the following is the greatest?
a. 3%5E210
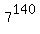
b. 7%5E140
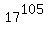
c. 17%5E105
d. 31%5E84
---------------
3^210 = 9^105, obviously less than 17^105, so a is eliminated.
-------
Using a calculator:
7^140 = 2.059e118
17^105 = 1.57e129
31^84 = 1.88e125
-----
c wins again.
======================
You can change them all to the same base, eg, 7, but that would require either logs or a calculator.
----
eg,
7^140 = (2^2.8)^140 = 2^392
-------------
ooooooooooooooh, John's answer is cool.
I might have figured that out eventually.
I should have spotted that 3, 7, 17 & 31 are all 2^n plus or minus 1.
In short, his solution is elegant.
Probably with assistance from Satan, since we all know god is stupid.

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


We can eliminate a for the reason Alan gave.

Then



By the binomial theorem, and



Notice that in the expansion of , the signs alternate, but in the expansion of the signs are all positive. Therefore



Similarly, the first term of will be and the terms will alternate, hence



Therefore, answer c, as Alan's calculator confirms.

John

My calculator said it, I believe it, that settles it