SOLUTION: Test the series 1/(1*2*3) + 3/(2*3*4) + 5/(3*4*5) + ... for convergence.

Algebra ->  Sequences-and-series -> SOLUTION: Test the series 1/(1*2*3) + 3/(2*3*4) + 5/(3*4*5) + ... for convergence.      Log On


   

Question 977051: Test the series 1/(1*2*3) + 3/(2*3*4) + 5/(3*4*5) + ... for convergence.
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
Test the series 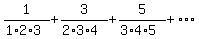for convergence or divergence.
The nth term is %282n-1%29%2F%28n%28n%2B1%29%28n%2B2%29%29

The degree of the denominator is 2 more than the degree of the numerator,
so we use the limit comparison test to the p-series with p=2,


which converges.









The degrees of numerator and denominator are the same,
the leading coefficient of the numerator is 2 and the
leading coefficient of the denominator is 1, so the
limit is 2/1 or 2.  Therefore the series converges.

Actually it converges to 3/4, but that takes more work to
discover that.

Edwin