Question 976927: An ice cream vendor sells three flavors: chocolate, strawberry, and vanilla. Forty five percent of the sales are chocolate, while 30% are strawberry, with the rest vanilla flavored. Sales are by the cone or the cup. The percentages of cones sales for chocolate, strawberry, and vanilla, are 75%, 60%, and 40%, respectively. For a randomly selected sale, define the following events:
= chocolate chosen
= strawberry chosen
= vanilla chosen
= ice cream on a cone
ice cream in a cup
Find the probability that the ice cream was strawberry flavor, given that it was sold on a cone
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's think of what happens for every 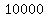 servings of ice cream sold. servings of ice cream sold.
For every 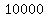 servings of ice cream sold, servings of ice cream sold,
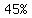 , or , or  are chocolate, are chocolate,
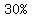 , or , or  are strawberry, are strawberry,
and the remaining  , or , or  are vanilla. are vanilla.
Of the 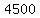 servings of chocolate ice cream sold, servings of chocolate ice cream sold,
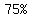 , or , or  were served in cones, were served in cones,
while the other  were served in cups. were served in cups.
Of the  servings of strawberry ice cream sold, servings of strawberry ice cream sold,
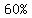 , or , or  were served in cones, were served in cones,
while the other  were served in cups. were served in cups.
Of the  servings of vanilla ice cream sold, servings of vanilla ice cream sold,
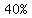 , or , or  were served in cones, were served in cones,
while the other  were served in cups. were served in cups.
We knew, without calculations that
the probability of a serving being chocolate is  , ,
the probability of a serving being strawberry is  , and , and
the probability of a serving being vanilla is  . .
Since out of 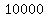 servings, there were servings, there were
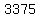 chocolate ice cream cones, chocolate ice cream cones,
 strawberry ice cream cones, and strawberry ice cream cones, and
 vanilla ice cream cones, vanilla ice cream cones,
the total number of cones served was  . .
So, the probability of a serving being a cone is  . .
Of course, that makes the probability of a serving being ice cream in a cup
 . .
Since of the 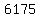 cones served, cones served,
 were strawberry ice cream cones, were strawberry ice cream cones,
the probability that the ice cream was strawberry flavor, given that it was sold on a cone is
 (rounded). (rounded).
, , and 40%,
|
|
|