Question 976543: How should I start this problem?
Find all rational zeros of the polynomial, and then find the irrational zeros, if any. Whenever appropriate, use the Rational Zeros Theorem, the Upper and Lower Bounds Theorem, Descartes' Rule of Signs, the quadratic formula, or other factoring techniques. (Enter your answers as comma-separated lists. If an answer does not exist, enter DNE.)
P(x) = 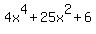
Found 2 solutions by Boreal, josgarithmetic:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! 4x^4 + 25x^2 +6=0
(4x^2+1)(x^2+6)=0 Treat it like a quadratic. Then see what the roots are.
4x^2=-1
x^2=(-1/4)
x=+/- (1/2)i
x^2=-6, x= +/- I sqrt(6)
This should graph like a quadratic with +x^2, since as x increases negatively or positively, y increases without bound. The y-intercept is (0,6), and there are no rational or irrational roots. It won't touch the y-axis. The lowest value is at the y-intercept, since any positive or negative x will increase the value of the function from 0.

Check =1/16*1*4 + (-1)*25*(1/4)+6=(1/4)-6(1/4)+6=0
i sqrt(6)^4=36
i sqrt (6)=-6
4*36-25(-6)+6=0
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
You can put this solution on YOUR website! You will find among possible rational and real roots, NO real roots. Try according to synthetic division and rational roots theorem, testing plus and minus of 1,2,3,6, 1/2, 1/4, 3/2,3/4. None will give zero remainder.
Solving for x^2 using general solution for quadratic formula, find  or or  . .
From these, continue on to find x values for the four imaginary roots.
Roots are 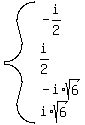 . .
|
|
|