SOLUTION: please a need help with this QUESTION (a)prove that the equation mx(x^2+2x+3) = x^2-2x-3 has exactly one real root if m=1 and exactly 3 real roots if m=-2/3. (b) prove that

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: please a need help with this QUESTION (a)prove that the equation mx(x^2+2x+3) = x^2-2x-3 has exactly one real root if m=1 and exactly 3 real roots if m=-2/3. (b) prove that      Log On


   

Question 976266: please a need help with this
QUESTION
(a)prove that the equation mx(x^2+2x+3) = x^2-2x-3 has exactly one real root if m=1 and exactly 3 real roots if m=-2/3.
(b) prove that tan t = sin2t/1+cos2t
and hence obtain the value of tan 15 degrees and 45 degrees and express the result in standard from

THANKS


Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
THE EASY ONE:
(b) prove that tan t = sin 2t/(1+cos 2t) or tan%28t%29=sin%282t%29%2F%281%2Bcos%282t%29%29 .
(Parentheses matter because sin 2t/(1+cos 2t)=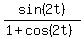sin%282t%29%2F%281%2Bcos%282t%29%29 ,
but 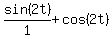sin%282t%29%2F1%2Bcos%282t%29 ).
sin 2t/1+cos 2t 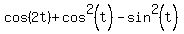=sin%282t%29=2sin%28t%29cos%28t%29 and cos%282t%29%2Bcos%5E2%28t%29-sin%5E2%28t%29 are popular trigonometric identities.
tan%28t%29=sin%28t%29%2Fcos%28t%29 and cos%5E2%28t%29%2Bsin%5E2%28t%29=1<--->cos%5E2%28t%29=1-sin%5E2%28t%29 even better known.
If we substitute, we get
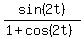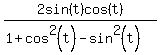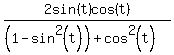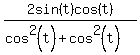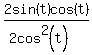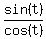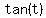
sin%282t%29%2F%281%2Bcos%282t%29%29=2sin%28t%29cos%28t%29%2F%281%2Bcos%5E2%28t%29-sin%5E2%28t%29%29=2sin%28t%29cos%28t%29%2F%28%281-sin%5E2%28t%29%29%2Bcos%5E2%28t%29%29=2sin%28t%29cos%28t%29%2F%28cos%5E2%28t%29%2Bcos%5E2%28t%29%29=2sin%28t%29cos%28t%29%2F%282cos%5E2%28t%29%29=sin%28t%29%2Fcos%28t%29=tan%28t%29

THE OTHER PROBLEM:
(a)prove that the equation mx(x^2+2x+3) = x^2-2x-3 has exactly one real root if m=1 and exactly 3 real roots if m=-2/3.
mx%28x%5E2%2B2x%2B3%29+=+x%5E2-2x-3<--->mx%28x%5E2%2B2x%2B3%29-x%5E2%2B2x%2B3=0<--->mx%5E3%2B%282m-1%29x%5E2%2B%283m%2B2%29x%2B3=0 is a cubic equation,
and cubic equations are easy to solve only when the teacher designs them so that they will be easy to solve.
The roots we look for are the zeros of the cubic polynomial P%28x%29=mx%5E3%2B%282m-1%29x%5E2%2B%283m%2B2%29x%2B3 .
In general, to know how many roots the cubic polynomial has, and to find their approximate values we can use calculus (or a graphing calculator).

When m=-2%2F3 , .
In the case of this cubic polynomial, we can actually find all three zeros easily,
because with P%28x%29=%28-2%2F3%29x%5E3%2B%28-7%2F3%29x%5E2%2B3 ,
P%281%29=%28-2%2F3%29%2B%28-7%2F3%29%2B3=-9%2F3%2B3=-3%2B3=0 , so x=1 is one of the zeros,
so %28x-1%29 is a factor of P%28x%29 and dividing we find that
P%28x%29=%28-2%2F3%29x%5E3%2B%28-7%2F3%29x%5E2%2B3=%28x-1%29%28%28-2%2F3%29x%5E2-3x-3%29 .
So, the other two real zeros (if any) would be the solutions to
%28-2%2F3%29x%5E2-3x-3=0<--->-2x%5E2-9x-9=0<--->2x%5E2%2B9x%2B9=0<--->%282x%2B3%29%28x%2B3%29=0 ,
which are x=-3%2F2 and x=-3 .

When m=1 , P%28x%29=x%5E3%2Bx%5E2%2B5x%2B3 ,
and I do not see an easy algebra way to figure out if that polynomial has 3 real zeros.
There may be a simpler algebra way to prove it has only one,
but I keep thinking calculus.
That bothers me, because I suspect there is a simpler (and therefore better) solution.

A cubic function, f%28x%29 , may have a graph like this graph%28200%2C200%2C1%2C5%2C1%2C5%2Cx%5E3-9x%5E2%2B27x-24%29 , or this graph%28200%2C200%2C1%2C5%2C1%2C5%2C-x%5E3%2B9x%5E2-27x%2B30%29 , or this graph%28200%2C200%2C5%2C15%2C5%2C95%2Cx%5E3-29x%5E2%2B285x-900%29 ,
with no relative maximum or minimum,
and then it would cross the x-axis (making f%28x%29=0 ) just for only one value of x .
Then, the equation f%28x%29=0 would have exactly one real root.
Cubic polynomials can also have graphs like this 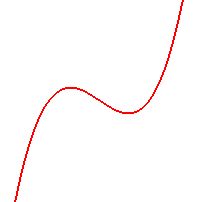graph%28200%2C200%2C4%2C8%2C3%2C9%2Cx%5E3-18x%5E2%2B107x-204%29 , or this graph%28200%2C200%2C4%2C8%2C3%2C9%2C-x%5E3%2B18x%5E2-107x%2B216%29 , with one maximum and one minimum,
and in that case the graph may cross/touch the x-axis at one, two, or three points,
as in graph%28200%2C200%2C4%2C8%2C-3%2C1%2Cx%5E3-18x%5E2%2B107x-211%29 , or graph%28200%2C200%2C4%2C8%2C-3%2C1%2Cx%5E3-18x%5E2%2B107x-210.3849%29 , or graph%28200%2C200%2C4%2C8%2C-2%2C2%2Cx%5E3-18x%5E2%2B107x-210%29 .
In those cases, the equation f%28x%29=0 would have respectively one real root, or two, or three.
We would want to know if the maximum and minimum values of f%28x%29
are both positive, or both negative (one root), or
one is zero (two roots), or
one is positive and the other negative (3 roots).
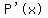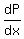We can figure out if P%28x%29=mx%28x%5E2%2B2x%2B3%29-x%5E2%2B2x%2B3=mx%5E3%2B%282m-1%29x%5E2%2B%283m%2B2%29x%2B3 has a maximum and a minimum by looking at its derivative, %22P+%27+%28+x+%29%22 or dP%2Fdx .
The derivative will be a quadratic function, and its real zeros (if any) indicate maximum and minimum.
With P%28x%29=mx%5E3%2B%282m-1%29x%5E2%2B%283m%2B2%29x%2B3 , dP%2Fdx=3mx%5E2%2B2%282m-1%29x%2B%283m%2B2%29 .
When m=1 , P%28x%29=x%5E3%2Bx%5E2%2B5x%2B3 has the derivative
dP%2Fdx=3x%5E2%2B2x%2B5 , which has no real zeros.
dP%2Fdx=3x%5E2%2B2x%2B5%3E0 for all values of x ,
so P%28x%29=x%5E3%2Bx%5E2%2B5x%2B3 is a continuously increasing function that must have exactly one real zero.
That zero must be between x=-1 and x=0 , because
P%28-1%29=%28-1%29%5E3%2B%28-1%29%5E2%2B5%28-1%29%2B3=-1%2B1-5%2B3=-2 and P%280%29=0%5E3%2B0%5E2%2B5%280%29%2B3=3 .

NOTE:
When m=-2%2F3 , .
If we had not found the three roots of P%28x%29=0 so easily,
we would look at the derivative for information,.
dP%2Fdx=-2x%5E2%2B2%28-7%2F3%29x=-2x%28x%2B7%2F3%29 , which has the real zeros x=-7%2F3 and x=0 .
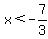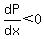For x%3C-7%2F3 and for x%3E0 , dP%2Fdx%3C0 and P%28x%29=%28-2%2F3%29x%5E3%2B%28-7%2F3%29x%5E2%2B3 decreases.
For 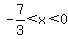-7%2F3%3Cx%3C0 , dP%2Fdx%3E0 and P%28x%29=%28-2%2F3%29x%5E3%2B%28-7%2F3%29x%5E2%2B3 increases.
P%28x%29=%28-2%2F3%29x%5E3%2B%28-7%2F3%29x%5E2%2B3 looks like this graph%28200%2C200%2C4%2C8%2C3%2C9%2C-x%5E3%2B18x%5E2-107x%2B216%29 .
There is a maximum at x=0, with P%280%29=3 ,
and a minimum at x=-7%2F3 .
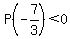If P%28-7%2F3%29%3C0 , there are 3 zeros.
,
so there are 3 zeros:
one at some point with 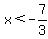x%3C-7%2F3 ,
another one for some point with 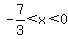-7%2F3%3Cx%3C0 ,
and one for x%3E0 .