Question 976010: How do I graph y=(3.4)abs((.7)(x-4))+1 step by step using absolute value transformation?
I understand that you should try to start with y=abs(x)
and that +1 means that the graph will be shifted by 1 up
and that -4 means that I will be shifting the graph to right by 4 units.
The problem is that I am not sure how to shrink the graph horizonally and by what number. What do I do with 3.4 and .7?
Answer by josgarithmetic(39625)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Critical x value will be for the absolute value part to be 0. That happens at x=4. The graph has two branches. For 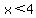 , and for , and for 
For  , expression inside abs val is positive or zero. , expression inside abs val is positive or zero.



 -----and you ONLY want the part where -----and you ONLY want the part where  ; NOTHING to the left. ; NOTHING to the left.
For 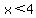 , expression inside the abs val is NEGATIVE. , expression inside the abs val is NEGATIVE.



 ------and you ONLY want the part to the left of ------and you ONLY want the part to the left of  ; nothing to the right. ; nothing to the right.

DISCUSSION OF TRANSFORMATION
The equation and graph fundamentally starts from  . This would be a "V" shaped figure, with the sharp corner at the origin, and both parts are above the x-axis, and therefore, y is non-negative everywhere. Shift this 4 units to the right, and 1 unit up, and you are at . This would be a "V" shaped figure, with the sharp corner at the origin, and both parts are above the x-axis, and therefore, y is non-negative everywhere. Shift this 4 units to the right, and 1 unit up, and you are at  . Same shape, just shifted so the vertex is now at (4,1), the sharp point of the "V". . Same shape, just shifted so the vertex is now at (4,1), the sharp point of the "V".
-
The factor, 0.7, squashes the graph vertically; and then the factor 3.4, stretches the graph vertically, MORE SO than the factor of the 0.7 did. This combination of factors only affects the slope or slopes of each branch. The combined factor for this is  ; overall, this stretches the graph of ; overall, this stretches the graph of  vertically; but still same vertex or sharp point at (4,1). The factor is not arranged to affect the "1". vertically; but still same vertex or sharp point at (4,1). The factor is not arranged to affect the "1".
|
|
|