Question 975805: Vehicle A is traveling at the same speed as vehicle B. Both are going 100km/hr. Vehicle A is 50 feet behind Vehicle B. If Vehicle A accelerates to 134 km/hr in 5 seconds, how long would it take to travel 50 feet past vehicle B?
or
at what speed would vehicle A have to get to, if it reached 50 feet passed Vehicle B in 5 seconds?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! INTERPRETATION:
Initially, vehicles A and B traveling at the same speed of 100km/h,
with vehicle A 50 feet behind Vehicle B.
Then, at a certain time, vehicle A accelerates at a constant rate of acceleration.
For the first question, vehicle A accelerates for 5 seconds until it reaches 134 km/hr,
and then continues at that speed until it is 50 feet ahead of vehicle B.
We want to know how long it took for the entire passing maneuver.
For the second question, vehicle A accelerates at a faster rate, so that it gets to be 50 feet ahead of vehicle B in just 5 seconds.
We want to know what was its final speed at the end of those 5 seconds.
The problem is complicated by the fact that speeds are measured in km/h,
times are measured in seconds,
and distances are measured in feet,
so that we have to make conversions.
THE FIFTH GRADER SOLUTION:
From the point of view of vehicle B, all speeds are 100 km/hr less,
so that vehicle B is not moving, and vehicle A is accelerating from 0km/h to 34 km/h for the first question,
and to a less impressive velocity for the second question.
From the point of view of vehicle B, for both questions,
vehicle A moves only 100 ft during the passing maneuver:
vehicle A is initially 50ft behind vehicle B,
and travels 100ft until it is 50 ft ahead of vehicle B.
We can take that point of view for the calculations,
and we would only need to add 100km/h to the second question answer.
When a vehicle accelerates at a constant rate, its average speed is the average of the initial and final speed.
For the first question, the final constant speed (after 5 seconds) is
134km/h - 100km/h = 34km/h,
and the average speed during the 5 seconds of acceleration is
 ,
so it is as if vehicle A was moving at  for those first 5 seconds, and then continues at .
In feet per second, those speeds are:
  (rounded) and
  (rounded)
How far does vehicle A travel for those first 5 seconds?
 (rounded).
At that point, from the point of view of vehicle B,
vehicle A still has to travel an additional
 at the apparent final speed of
 (rounded) .
How long will it take to cover that apparent  distance?
 (rounded).
So, the whole passing maneuver would take
 .
For the second question, the apparent average speed needed
to advance an apparent distance of 100 ft in 5 seconds is  .
That average speed is the average of 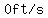 and the apparent final speed.
so the apparent final speed is 
In km/h that apparent final speed is
 (rounded).
That is the apparent speed at the end of 5 seconds as seen from
the point of view of vehicle B, which is moving at a constant speed of 100km/h.
From the point of view of a police car stopped on the shoulder of the road,
the final speed of vehicle A is
100km/h + 43.89km/h =  (rounded).
|
|
|
