Question 975208: What is the probability that 15 rolls of a fair die will show 5 threes?
Found 3 solutions by Boreal, solver91311, Edwin McCravy:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! Probability of a 3 is (1/6)
This is a binomial with 15C5*(1/6)^5*(5/6)^10 = 0.0624
There are 15 rolls and 3003 different ways 5 threes can come up.
The overall probability is that time (1/6)^5 times and (5/6)^10 times.
The expected value would be 2.5, so this is reasonable.
While the numbers are too small to use the normal approximation, the variance is np(1-p)=75/36
The standard deviation would be about 1.35.
This is about 2 sd s above the mean, so again it is in the range of what one would expect.
Answer by solver91311(24713)  (Show Source):
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
I think what you want is a binomial probability, not what the others gave you.
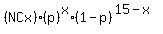N = number of trials = 15
x = number of times out of those to succeed = 5
p = the probability of 1 success in 1 trial = 1/6
NCx =  
15C5 = 
 
Or else on TI-83 or 84
Press 2ND,
Press VARS,
scroll down to highlight binompdf(,
Press ENTER
--------------------
If you have newer model, make it read
trials: 15
p:1/6
x value:5
Paste
Highlight Paste
press ENTER
You will see
binompdf(15,1/6,5)
---------------------
If you have older model, you just see
binompdf(
make it read
binompdf(15,1/6,5)
--------------------
press ENTER
Read .0623715619
Edwin
|
|
|
