 There is no way to tell which of these triangles that is desired.
So we do both.
Either way, the first thing to do is draw the altitude,(in green)
which splits the base into two segments each half as long as the
original base, 9.4/2 = 4.7 on the left and 16/2 = 8 on the right.
The green altitude divides the isosceles triangles into two
congruent right triangles, so that we can use trig ratios.
There is no way to tell which of these triangles that is desired.
So we do both.
Either way, the first thing to do is draw the altitude,(in green)
which splits the base into two segments each half as long as the
original base, 9.4/2 = 4.7 on the left and 16/2 = 8 on the right.
The green altitude divides the isosceles triangles into two
congruent right triangles, so that we can use trig ratios.
 In each we know the ADJACENT SIDE and the HYPOTENUSE, so we
use COSINE.
In the figure on the left, we have
In each we know the ADJACENT SIDE and the HYPOTENUSE, so we
use COSINE.
In the figure on the left, we have




 We use our calculator and find
We use our calculator and find 

 Since all three angles of a triangle = 180°, we find the vertex angle:
180°-2(72.91740297°) = 34.16519407°
So the angles in the triangle on the left are:
Base angles = 72.91740297° each, vertex angle = 34.16519407°
Rounded to the nearest degree, 73°, 73°, 34°
-------------------------------------------
In the figure on the right, we have
Since all three angles of a triangle = 180°, we find the vertex angle:
180°-2(72.91740297°) = 34.16519407°
So the angles in the triangle on the left are:
Base angles = 72.91740297° each, vertex angle = 34.16519407°
Rounded to the nearest degree, 73°, 73°, 34°
-------------------------------------------
In the figure on the right, we have




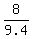 We use our calculator and find
We use our calculator and find 

 Since all three angles of a triangle = 180°, we find the vertex angle:
180°-2(31.67243343°) = 116.6551331°
So the angles in the triangle on the right are:
Base angles = 31.67243343° each, vertex angle = 116.6551331°
Rounded to the nearest degree, 32°, 32°, 117°
[Notice that adding the rounded angles gives 181° not 180°, demonstrating
that rounding always introduces error. It's a matter of sacrificing
accuracy for convenience.]
Edwin
Since all three angles of a triangle = 180°, we find the vertex angle:
180°-2(31.67243343°) = 116.6551331°
So the angles in the triangle on the right are:
Base angles = 31.67243343° each, vertex angle = 116.6551331°
Rounded to the nearest degree, 32°, 32°, 117°
[Notice that adding the rounded angles gives 181° not 180°, demonstrating
that rounding always introduces error. It's a matter of sacrificing
accuracy for convenience.]
Edwin