SOLUTION: Solve the system: 2x+3y+6z=2 -x+y+z=0 I tried by the equation {{{ X=A^(-1)B }}} Please help me solve it..

Algebra ->  Matrices-and-determiminant -> SOLUTION: Solve the system: 2x+3y+6z=2 -x+y+z=0 I tried by the equation {{{ X=A^(-1)B }}} Please help me solve it..       Log On


   

Question 974842: Solve the system: 2x+3y+6z=2
-x+y+z=0
I tried by the equation +X=A%5E%28-1%29B+
Please help me solve it..
Answer by Edwin McCravy(20063) About Me  (Show Source):
You can put this solution on YOUR website!
Solve the system: 2x+3y+6z=2
-x+y+z=0
I tried by the equation +X=A%5E%28-1%29B+
Please help me solve it..
This system has more unknowns than equations, so it is labeled an
"under-determined system", so it has infinitely many solutions.
The coefficient matrix is not a square matrix, thus it has no
inverse.  If you've studied left-inverse and right-inverses,
you may be able to get the general solution for the infinite
set of solutions that way, but you can get that easier just by 
ordinary methods:


system%282x%2B3y%2B6z=2%2C%0D%0A-x%2By%2Bz=0%29

Multiply 2nd equation by 2

system%282x%2B3y%2B6z=2%2C%0D%0A-2x%2B2y%2B2z=0%29

Add them

5y%2B8z+=+2
5y+=+2-8z
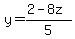y+=+%282-8z%29%2F5

Substitute in

-x%2By%2Bz=0
-x%2B%282-8z%29%2F5%2Bz=0
-5x%2B%282-8z%29%2B5z=0
-5x%2B2-8z%2B5z=0
-5x%2B2-3z=0
-5x=-2%2B3z
5x=2-3z
x=%282-3z%29%2F5

There are infinitely many solutions.  Just substitute arbitrary 
values for z in the expressions above.  Here, I'll set up a 
computer program to generate some of them:

If you choose z=-21, then substituting, x=%282-3%28-21%29%29%2F5+=+%282-%28-63%29%29%2F5=%2865%29%2F5=13
Also, y=%282-8%28-21%29%29%2F5+=+%282-%28-168%29%29%2F5=%28170%29%2F5=34

If you choose z=-16, then substituting, x=%282-3%28-16%29%29%2F5+=+%282-%28-48%29%29%2F5=%2850%29%2F5=10
Also, y=%282-8%28-16%29%29%2F5+=+%282-%28-128%29%29%2F5=%28130%29%2F5=26

If you choose z=-11, then substituting, x=%282-3%28-11%29%29%2F5+=+%282-%28-33%29%29%2F5=%2835%29%2F5=7
Also, y=%282-8%28-11%29%29%2F5+=+%282-%28-88%29%29%2F5=%2890%29%2F5=18

If you choose z=-6, then substituting, x=%282-3%28-6%29%29%2F5+=+%282-%28-18%29%29%2F5=%2820%29%2F5=4
Also, y=%282-8%28-6%29%29%2F5+=+%282-%28-48%29%29%2F5=%2850%29%2F5=10

If you choose z=-1, then substituting, x=%282-3%28-1%29%29%2F5+=+%282-%28-3%29%29%2F5=%285%29%2F5=1
Also, y=%282-8%28-1%29%29%2F5+=+%282-%28-8%29%29%2F5=%2810%29%2F5=2

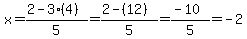If you choose z=4, then substituting, x=%282-3%284%29%29%2F5+=+%282-%2812%29%29%2F5=%28-10%29%2F5=-2
Also, y=%282-8%284%29%29%2F5+=+%282-%2832%29%29%2F5=%28-30%29%2F5=-6

If you choose z=9, then substituting, x=%282-3%289%29%29%2F5+=+%282-%2827%29%29%2F5=%28-25%29%2F5=-5
Also, y=%282-8%289%29%29%2F5+=+%282-%2872%29%29%2F5=%28-70%29%2F5=-14

If you choose z=14, then substituting, x=%282-3%2814%29%29%2F5+=+%282-%2842%29%29%2F5=%28-40%29%2F5=-8
Also, y=%282-8%2814%29%29%2F5+=+%282-%28112%29%29%2F5=%28-110%29%2F5=-22

If you choose z=19, then substituting, x=%282-3%2819%29%29%2F5+=+%282-%2857%29%29%2F5=%28-55%29%2F5=-11
Also, y=%282-8%2819%29%29%2F5+=+%282-%28152%29%29%2F5=%28-150%29%2F5=-30
 
I chose those value because they give integer solutions, however,
you can get fractional solutions by choosing other values for z.

Edwin