Question 974820: Please help me solve this problem; i already tried and got B. 10.00, however this is not right because I got it wrong.
If the areas of two similar hexagons are to each other as 5 : 2, and one side of the first hexagon is 25, what is the corresponding side in the other hexagon? Round your answer to two decimal places.
A. 3.16
B. 10.00
C. 15.81
D. 250.00
Found 2 solutions by Boreal, MathTherapy:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! I was wrong.
another way is it is 2.6 x the side length squared.
Area of the first is 625 *2.96=1850
The second is 40% of that or 740
Divide by 2.96=250
Take the square root15.81
The other way is through 6 equilateral triangles.
Area of an equilateral triangle is
[(sart 3)/4] *a^2, where a is the side.
This is 0.433 a^2.
6 equilateral triangles have 2.598 *a^2. That is where the 2.6 came from.
C is the answer.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please help me solve this problem; i already tried and got B. 10.00, however this is not right because I got it wrong.
If the areas of two similar hexagons are to each other as 5 : 2, and one side of the first hexagon is 25, what is the corresponding side in the other hexagon? Round your answer to two decimal places.
A. 3.16
B. 10.00
C. 15.81
D. 250.00
If 25 is one side of the larger hexagon, then corresponding side of smaller hexagon is:
15.8113883 ≈  (CHOICE C) (CHOICE C)
Solution:
Ratio of sides of LARGER and SMALLER hexagons, equals SQUARE ROOT of ratio of LARGER and SMALLER hexagons' areas, OR simply:
With R being ratio of larger hexagon's to smaller hexagon's sides, we get:
 , or 1.58113883 , or 1.58113883
Thus, side of smaller hexagon = 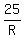 , or , or 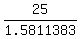 , or 15.811383 ≈ , or 15.811383 ≈ 
|
|
|