Question 974752: a box contains $7.15 in nickels, dimes, and quaters,. There are 42 coins in all and the combined total of nickles and dimes is 2 less than the total number of quaters. Find the number of each type of coin, using systems of equations, and showing work.
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a box contains $7.15 in nickels, dimes, and quaters,. There are 42 coins in all and the combined total of nickles and dimes is 2 less than the total number of quaters. Find the number of each type of coin, using systems of equations, and showing work.
Let number of nickels, dimes, and quarters, be N, D, and Q, respectively
Then we get: N + D + Q = 42 ------- eq (i)
Also, N + D = Q - 2_____N + D - Q = - 2 ------- eq (ii)
2Q = 44 ------ Subtracting eq (ii) from eq (i)
Q, or number of quarters = 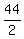 , or , or 
N + D + 22 = 42 ------- Substituting 22 for Q in eq (i)
N + D = 20
N = 20 - D
Since all coins total $7.15, we then get:
.05N + .1D + .25(Q) = 7.15
.05(20 - D) + .1D + .25(22) = 7.15
1 - .05D + .1D + 5.5 = 7.15
- .05D + .1D + 1 + 5.5 = 7.15
.05D + 6.5 = 7.15
.05D = .65
D, or number of dimes = 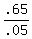 , or , or 
N = 20 - D
N = 20 - 13 ------ Substituting 13 for D
N, or number of nickels = 
|
|
|