SOLUTION: A rocket was fired with an initial velocity of 25 meters per second from a platform 10m above ground. a)when will the rocket reach its maximum height? b)What is the maximum heigh

Algebra ->  Functions -> SOLUTION: A rocket was fired with an initial velocity of 25 meters per second from a platform 10m above ground. a)when will the rocket reach its maximum height? b)What is the maximum heigh      Log On


   

Question 974255: A rocket was fired with an initial velocity of 25 meters per second from a platform 10m above ground.
a)when will the rocket reach its maximum height?
b)What is the maximum height of the rocket in the air?
c)For how long does the rocket stay at or above 20 meters?
d)When does the rocket strike the ground?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
If you are not given the function that represents height as a function of time, this is a physics problem, rather than an algebra problem.
A friendly physics problem would say that you can use g=10m%2Fs%5E2 .
Lacking such show of friendship, we are obligated to use the cumbersome g=9.8m%2Fs%5E2 that is a better approximation of g on/near Earth's surface.

If we could use g=10m%2Fs%5E2 ,
parts a) and b)are easy mental math:
a) The rocket reach its maximum height when its upwards velocity becomes 0 ,
and if it starts at 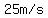%2225+m+%2F+s%22 ,
decreasing at a rate of 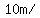%2210+m+%2F%22s%5E2=%2210+m+%2F+s+%2Fs%22 ,
that would take %2225+m+%2F+s%22%2F%2210+m+%2F+s+%2Fs%22=2.5s
b)Since the upwards velocity was decreasing linearly (at a constant rate),
the average upwards velocity for the upwards flight is the average of the initial and final velocities,
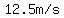%28%2225+m+%2F+s%22%2B%220+m+%2F+s%22%29%2F2=%2212.5+m+%2F+s%22 .
during the 2.5s upwards flight with an average velocity of %2212.5+m+%2F+s%22 ,
the rocket traveled 2.5s%28%2212.5+m+%2F+s%22%29=31.25m .
Since the rocket started its upwards flight at a height of 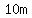10m ,
its maximum height is 10m%2B31.25m=41.25m .

If you must use g=9.8m%2Fs%5E2 ,
the calculations are the same,
but I suggest using a calculator.

For the rest,
h= height of the rocket above the ground, in m
h%5B0%5D= initial height of the rocket above the ground, in mt= time since launch, in seconds
v%5B0%5D= initial velocity, in m/s
g= acceleration of gravity, in m/s/s.
v= upwards velocity, in m/s
v=v%5B0%5D-gt
The average velocity in the interval [0,t] is
%28v%5B0%5D%2Bv%29%2F2=%28v%5B0%5D%2Bv%5B0%5D-gt%29%2F2=v%5B0%5D-gt%2F2
and consequently, the gain in height in the interval [0,t] is
DELTAh=t%28v%5B0%5D-gt%2F2%29=v%5B0%5Dt-gt%5E2%2F2 , so
h=h%5B0%5D%2Bv%5B0%5Dt-gt%5E2%2F2
The above equation can be used to find the answers to parts c) and d) .

If I can use g=%2210+m+%2F+s+%2F+s%22 ,
substituting that, along with h%5B0%5D=0 and v%5B0%5D=25 , i get
h=10%2B25t-5t%5E2
c) h=10%2B25t-5t%5E2%3E=20-->10%2B25t-5t%5E2-20%3E=0-->-5t%5E2%2B25t-10%3E=0-->-t%5E2%2B5t-2%3E=0
Since the solutions to -t%5E2%2B5t-2=0 are t=%285+%2B-+sqrt%2833%29%29%2F2
-t%5E2%2B5t-2%3E=0--->%285+%2B-+sqrt%2833%29%29%2F2%3C=t%3C=%285+%2B-+sqrt%2833%29%29%2F2
(An approximate decimal value may be expected as an answer).
d) h=10%2B25t-5t%5E2=0-->-t%5E2%2B5t%2B2%3E=0
The two solutions are t=%28-5+%2B-+sqrt%2833%29%29%2F2 , but
t=%28-5+-+sqrt%2833%29%29%2F2%3C0 does not make sense,
so the rocket gets down to ground level at t=%28-5+%2B+sqrt%2833%29%29%2F2 .
(An approximate decimal value may be expected as an answer).
If you must use g=9.8m%2Fs%5E2 ,
the calculations are the similar,
but I suggest using a calculator.