SOLUTION: 1) if x is a rational number and (x+1)^3 -(x-1)^3 / (x+1)^2 - (x-1)^2 = 2, then the sum of numerator and denominator of x is ? 2) if x^2 + y^2 + 1 = 2x, then x^3 + y^5 = ?

Algebra ->  Expressions -> SOLUTION: 1) if x is a rational number and (x+1)^3 -(x-1)^3 / (x+1)^2 - (x-1)^2 = 2, then the sum of numerator and denominator of x is ? 2) if x^2 + y^2 + 1 = 2x, then x^3 + y^5 = ?      Log On


   

Question 973934: 1) if x is a rational number and (x+1)^3 -(x-1)^3 / (x+1)^2 - (x-1)^2 = 2, then the sum of numerator and denominator of x is ?
2) if x^2 + y^2 + 1 = 2x, then x^3 + y^5 = ?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
2) If x^2+y^2+1=2x, then
x^2+y^2+1-2x=0 ---> (x^2-2x+1)+y^2=0 ---> (x-1)^2+y^2=0 ---> y=0 and x-1=0<-->x=1.
Then,
x^3 + y^5 = 1^2 + 0^2 =1 + 0 = 1

1) Did you really mean
(x+1)^3 -(x-1)^3 / (x+1)^2 - (x-1)^2 =%28x%2B1%29%5E3+-%28x-1%29%5E3+%2F+%28x%2B1%29%5E2+-+%28x-1%29%5E2= 2?
Or did you mean
[ (x+1)^3 -(x-1)^3 ] / [ (x+1)^2 - (x-1)^2 ]=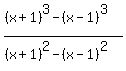%28%28x%2B1%29%5E3+-%28x-1%29%5E3%29%2F%28%28x%2B1%29%5E2+-+%28x-1%29%5E2%29= 2?
I like the 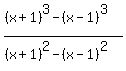%28%28x%2B1%29%5E3+-%28x-1%29%5E3%29%2F%28%28x%2B1%29%5E2+-+%28x-1%29%5E2%29 expression,
because it has a sort of elegant symmetry, and simplifies nicely.

You can expand all those cubes and squares and laboriously simplify.
We can also use special products to simplify the expression with less risk for mistakes.
If we make the system%28a=x%2B1%2Cb=x-1%29 to save some writing, we can simplify easier.
We know that a%5E3-b%5E3=%28a-b%29%28a%5E2%2Bab%2Bb%5E2%29 , that a%5E2-b%5E2=%28a-b%29%28a%2Bb%29 , and that %28a%2Bb%29%5E2=a%5E2%2B2ab%2Bb%5E2 .
So, .
So, going back to x ,
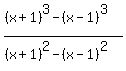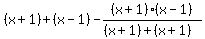%28%28x%2B1%29%5E3+-%28x-1%29%5E3%29%2F%28%28x%2B1%29%5E2+-+%28x-1%29%5E2%29=%28x%2B1%29%2B%28x-1%29-%28x%2B1%29%28x-1%29%2F%28%28x%2B1%29%2B%28x%2B1%29%29=2x-%28x%5E2-1%29%2F%282x%29=%284x%5E2-%28x%5E2-1%29%29%2F%222+x%22
=%284x%5E2-x%5E2%2B1%29%2F%222+x%22=%283x%5E2%2B1%29%2F%222+x%22

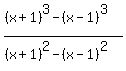, so if %28%28x%2B1%29%5E3+-%28x-1%29%5E3%29%2F%28%28x%2B1%29%5E2+-+%28x-1%29%5E2%29= 2,
%283x%5E2%2B1%29%2F%222+x%22=2-->3x%5E2%2B1=4x-->3x%5E2-4x%2B1=0-->%283x-1%29%28x-1%29=0-->system%28x=1%2F3%2C%22or%22%2Cx=1=1%2F1%29 .
Then, the sum of numerator and denominator of x is either 1%2B3=4 or 1%2B1=2 .


=
=
So, if %28x%2B1%29%5E3+-%28x-1%29%5E3+%2F+%28x%2B1%29%5E2+-+%28x-1%29%5E2=2 , then
%28x%5E5%2B4x%5E4%2B9x%5E3%2B15x%5E2%2B2x%2B1%29%2F%28x%5E2%2B2x%2B1%29=2-->%28x%5E5%2B4x%5E4%2B9x%5E3%2B15x%5E2%2B2x%2B1%29=2%28x%5E2%2B2x%2B1%29
-->%28x%5E5%2B4x%5E4%2B9x%5E3%2B15x%5E2%2B2x%2B1%29=2x%5E2%2B4x%2B2-->%28x%5E5%2B4x%5E4%2B9x%5E3%2B15x%5E2%2B2x%2B1%29-%282x%5E2%2B4x%2B2%29=0
-->x%5E5%2B4x%5E4%2B9x%5E3%2B15x%5E2%2B2x%2B1-2x%5E2-4x-2=0-->x%5E5%2B4x%5E4%2B9x%5E3%2B13x%5E2-2x-1=0

The rational number x=m%2Fn ,
where m and n are integers with no common factors,
that could be a solution to the equation above
has an m that is a factor of the independent term, -1 ,
and an n which is a factor of the leading coefficient, 1 .
So, x=1%2F1=%28-1%29%2F%28-1%29 or x=%28-1%29%2F1=1%2F%28-1%29 .
The problem with that, is that
for x=1 , x%5E5%2B4x%5E4%2B9x%5E3%2B13x%5E2-2x-1=1%2B4%2B9%2B13-2-1=24 ,
and x=-1 makes the denominator zero.
For x=-1 , %28x%2B1%29%5E2=0 , and
%28x%2B1%29%5E3+-%28x-1%29%5E3+%2F+%28x%2B1%29%5E2+-+%28x-1%29%5E2 is undefined.
My conclusion is that there is no rational value of x that will make
%28x%2B1%29%5E3+-%28x-1%29%5E3+%2F+%28x%2B1%29%5E2+-+%28x-1%29%5E2= 2