Question 973915: I have been asked to find the z-score for a normal distribution that has a mean of 100 and standard deviation of 8. x=108. So the z-score I got was 1. Now knowing that information I am supposed to determine the area or probability of p(x>108). I am not sure what to do. I honestly don't even know where to begin. If someone can help walk me through the steps or lead me in how to address this problem that would be wonderful because I have five questions similar to that with x>,
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website! I have been asked to find the z-score for a normal distribution that has a mean of 100 and standard deviation of 8. x=108. So the z-score I got was 1. Now knowing that information I am supposed to determine the area or probability of p(x>108). I am not sure what to do. I honestly don't even know where to begin. If someone can help walk me through the steps or lead me in how to address this problem that would be wonderful because I have five questions similar to that with x>,
A z score of 1 is correct, calculated as follows: 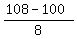
Dealing with z scores, I'm certain you have a book with a table of z scores. If you do, then look up for the
percentage under the bell curve for a z score of 1. If not, you can use the "NORMSDIST" function in MS excel
to find the percentage associated with a z score of 1. Either way, you should find it to be: .8413.
A percentage of .8413 or 84.13% THOUGH, represents the area to the LEFT OF the x value of 108. Therefore,
the area to the RIGHT of the x value of 108, or x > 108 is: 1 - .8413, or  , or , or  % %
|
|
|