SOLUTION: Please help!!!! What are all the solutions of the equation cos(2x)+1=sin(2x) in interval [0,2pi)?

Algebra ->  Trigonometry-basics -> SOLUTION: Please help!!!! What are all the solutions of the equation cos(2x)+1=sin(2x) in interval [0,2pi)?      Log On


   

Question 973867: Please help!!!!
What are all the solutions of the equation cos(2x)+1=sin(2x) in interval [0,2pi)?
Found 2 solutions by Edwin McCravy, KMST:
Answer by Edwin McCravy(20060) About Me  (Show Source):
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Let+me+write+%7B%7B%7Bu=2x for short, that way, I can simply write
cos%28u%29%2B1=sin%28u%29
Since cos%28u%29%3E=-1 , sin%28u%29=cos%28u%29%2B1%3E=-1%2B1=0 .
Also, since sin%28u%29%3C=1, sin%28u%29=cos%28u%29%2B1%3C=1 ---> cos%28u%29%3C=1-1=0 .
With a negative cosine and a positive sine, u must be in quadrant II.
Maybe pi%2F2%3C=u%3C=pi as in or maybe even pi%2F2%2B2pi=5pi%2F2%3C=u%3C=3pi as in
Knowing that sin%28u%29%3E=0 ,
cos%28u%29%2B1=sin%28u%29--->cos%28u%29%2B1=sqrt%281-cos%5E2%28u%29%29--->%28cos%28u%29%2B1%29%5E2=1-cos%5E2%28u%29--->cos%28u%29%5E2%2B2cos%28u%29%2B1=1-cos%5E2%28u%29--->cos%28u%29%5E2%2B2cos%28u%29=-cos%5E2%28u%29--->2cos%28u%29%5E2%2B2cos%28u%29=0--->2cos%28u%29%28cos%28u%29%2B1%29=0 .
So, either cos%28u%29=0 , or cos%28u%29%2B1=0<--->cos%28u%29=-1 .

For quadrant II, cos%28u%29=0 ---> system%28u=pi%2F2%2C%22or%22%2Cu=5pi%2F2%29 , and
u=2x=pi%2F2 means highlight%28x=pi%2F4%29 , while
u=2x=5pi%2F2 means highlight%28x=5pi%2F4%29 .

For quadrant II, cos%28u%29=-1 ---> system%28u=pi%2C%22or%22%2Cu=3pi%29 , and
u=2x=pi means highlight%28x=pi%2F2%29 , while
u=2x=3pi means highlight%28x=3pi%2F2%29 .

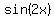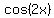If we think that sin%282x%29 and cos%282x%29 have a period of pi ,
or if we graph red%28y=cos%282x%29%2B1%29 and green%28y=sin%282x%29%29 we see that it makes a lot of sense:
graph%28700%2C300%2C-0.3%2C6.7%2C-1.1%2C2.2%2Ccos%282x%29%2B1%2Csin%282x%29%29