|
Question 973815: Hello! I really need help with this! My teacher never gave us a lesson on this, so I am struggling through! It is all pretty much how to identify a conic, but I do not really get what that means or how to do it. Here are a few of the problems, but if you want, you can only use one of them to show me how to do the rest.
identify the conic represented by the equation x^2-6x = y+3
identify the conic with the equation 3x^2 - y^2 - 7x + 2 = 0
identify the conic section of the equation [(x-2)^2]/9 - [(y+2)^2]/4 = 1
please help me!!!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Conics with axes of symmetry parallel to the x-axis and/or y-axis are easy to identify and graph.
PARABOLAS have only one variable squared, and you can transform them into something like  or or  with some constants with some constants  , ,  , and , and  . .



 
ELLIPSES and CIRCLES have equations that can be transformed into something like

With  we get a circle: we get a circle:  <---> <---> . .
If 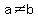 the circle gets stretched to make it longer in the direction of the variable atop that larger of the circle gets stretched to make it longer in the direction of the variable atop that larger of  and and  . .
If you see an  and a and a  that would both have a positive coefficient if they were on the same side of the equal sign, suspect an ellipse that would both have a positive coefficient if they were on the same side of the equal sign, suspect an ellipse
(you don't have one of those in your examples).
HYPERBOLAS have equations that can be transformed into something like
 or or  . .
 <---> <---> is already it that form (no need to transform it much). is already it that form (no need to transform it much).
Its axes of symmetry are the lines  and and  . .
It is centered at (2,-2).
Your other example takes a little more work to get it into that form,
but you may not need to do the transformation.
If the terms in  and and  have coefficients with opposite sign when they are on the same side of the equal sign, suspect a hyperbola. have coefficients with opposite sign when they are on the same side of the equal sign, suspect a hyperbola.







Now, I divide by 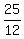 (or multiply times (or multiply times 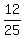 , same thing) to get , same thing) to get




That is really a hyperbola, because teachers usually do not try to trick you.
NOTE:
If the teacher wanted to trick you, he/she could give you something that had an  and a and a  , but transformed into something like , but transformed into something like
 <--> <--> <---> <---> <---> <---> , ,
and that graphs as just two lines that intersect,
but you can call that a degenerate hyperbola,
a hyperbola that degenerated into those two lines.
You could also have something that may have an  and a and a  with positive coefficients on the same side of the equal sign, with positive coefficients on the same side of the equal sign,
but when transformed turned out to be a "degenerate ellipse,"
that could be a single point (as for  ), ),
or no point at all (as for  ). ).
|
|
|
| |