Question 973731: Quite long: I have the answer already, I would like to make sure I did it correctly, thank you!
Ship it here is a comoany that specializes in shopping freght in medium sized boxes. The company limits the boxes that it will ship to those who's sum of the length, height and width is at least 100 cm but no more then a 1000. Gadgets to go is another comoany that ships their products in boxes which has integer dimensiones such that their length, width, height are in the rations 4:3:5. The largest they use to ship any product has a volume less then 2 cubic centimeters. Determine the dimensions of both the smallest and largest which can be shipped by gadgets to go and ship it here.
I basically took 4x+3x+5x=100 and 4x x 5x x 3x
From the on I used guess and check.
Here are my answers:
The largest box has: 128, 96 and 160 as their dimensions
Smallest: 36,27 and 45
Thank you!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Guess and check works easily if you can use a computer (preferably with a spreadsheet program),
or a graphing calculator,
but it is time consuming otherwise.
There is an algebra way to get to the solution.
You figured out that for the boxes to have dimensions (in centimeters) that are integers, and are in the ratio 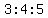 , ,
the dimensions (in centimeters) must be  , ,  , and , and  , ,
with  = a positive integer. = a positive integer.
That is one of the requirements of the company Gadgets To Go.
For a box meeting that requirement, the sum of the dimensions (in centimeters) is
 . .
For that box to meet the requirements of the company Ship It Here, it must be
 <---> <--->  . .
Since  =8.3333... and =8.3333... and 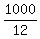 =83.3333... , =83.3333... ,
and  must be integer, it must be must be integer, it must be  . .
We calculate the volume (in cubic centimeters) of a box measuring  cm by cm by  cm by cm by  cm as cm as
 . .
For  , we get , we get  . .
That agrees with the dimensions you list for the smallest box.
For  , we get , we get  . .
Gadgets To Go seems to have a maximum volume limit lower than 34,307,220 cubic centimeters,
but "The largest they use to ship any product has a volume less then 2 cubic centimeters" does not make sense.
The smallest box Gadgets To Go would ship would measure 3 cm by 4 cm by 5 cm,
and its volume (in cubic centimeters) would be  . .
The volume of largest box Gadgets To Go would ship cannot be "less then 2 cubic centimeters."
If it were less than  cubic centimeters, cubic centimeters,
we would require
 <---> <--->  <---> <--->  . .
If it were that "The largest they use to ship any product has a volume less than 2 cubic meters" = 2,000,000 centimeters,
we would require  , and since , and since  , we would settle for integers such that , we would settle for integers such that  , ,
which meets the  requirement and would result in a largest box with requirement and would result in a largest box with
 . .
That agrees with the dimensions you list for the largest box.
|
|
|