|
Question 973649: The digital sum of an integer is the sum of all its digits. A digit sum sequence is a sequence of numbers that start with any integer and has each number after the first equal to the digital sum of the number before it. e.g. 7598, 29, 11, 2. Any digital sum sequence ends in a single digit number called the final digital sum or FDS.
Find and justify a rule that produces all 3 digit multiples of 7 with an FDS of 7
Find and justify a rule that produces all 3 digit multiples of 8 with an FDS of 8
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Find and justify a rule that produces all 3 digit multiples of 7 with an FDS of 7:
The FDS is the remainder of dividing a number by 9,
so a 3-digit number with an FDS of 7 can be written as
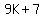 for some positive integer  .
If the number is also a multiple of 7,
then it can be written as 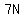 for some positive integer  .
So,
 ---> --->
That means that K must be a multiple of 7,
which could be written as  for some positive integer  .
Now we have that the number is
 ,
which gives us a simple rule to find all the multiples of 7 with an FDS of 7.
We start with  ,
because we need  for a 3-digit number, and
---> ---> ---> .
yields  ,
and that is our first 3-digit multiple of 7 with an FDS of 7.
Then we keep repeatedly adding  to get all the other 3-digit multiple of 7 with an FDS of 7,
until we get to  ,
which is the greatest 3-digit multiple of 7 with an FDS of 7,
because  ---> --->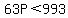
Find and justify a rule that produces all 3 digit multiples of 8 with an FDS of 8:
The same reasoning tells you that they will be numbers of the form
 .
So, we start with to get  ,
and we repeatedly add  all the way up to
 .
|
|
|
| |
