Question 973355: I have become stuck while brushing up on my algebra and unfortunately, I cannot contact any of my teachers because it is our summer break. Please help me, kindly tutors of algebra.com!
I know how to use the AC method, Perfect Square Trinomials, and how to plug in values into the General formula, but I don't know which method to use in solving this particular problem.
What are the factors of 
Another similar problem that I encountered is
Give the rational roots of the function 
Please show me a viable method that I can use to solve these types of problems.
Another is: Show the number of negative real zeroes of the function 
I broke the one question only rule because I have become quite desperate for some help, and I feel that the solutions to these three are quite related, somehow. Much thanks to the tutor that might help me! I will give a great review!
Answer by josgarithmetic(39620)   (Show Source):
You can put this solution on YOUR website! Factoring your first polynomial and your H(x) function are beyond the typical Intermediate
Algebra level. Make use of Rational Roots Theorem.
can be tested for possible roots, plus and minus 1,2,3,6. This can be done with
synthetic division. You could expect at most, three roots.
-
 is a root, giving remainder 0, and coefficients of quotient, 1,2,-3.
 is a root, giving remainder 0, and coefficients of quotient, 1,-1.
-
This gives you a factorization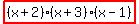 
The meaning of those last coefficients of 1,-1 is  , or as shown,  .
 may have any roots (need to test each) of again, plus and minus 1,2,3,6.
Testing for roots plus and minus 1,2,3 seem to give nonzero remainders. Maybe continue testing
for -6 and +6....
Neither give 0 remainder, so no rational roots.
H(x) may have irrational roots, but checking for them is harder. Other tests are possible
but are more lengthy.
-
Using a graphing tool, like putting y=10x^4+2x^2-x+6 into the text field of Google search engine
shows a fairly symmetric looking U shaped graph, and the minimum is above the x-axis everywhere,
so H(x) has no real roots. This also means no real irrational roots.
-
Note that there ARE more roots to check. numerators are plus or minus 1,2,3,6 and denominators
are plus and minus 1,2,5,10. I did not try the possible roots other than those for whole numbers.
You should expect up to FOUR complex roots.
You can try Rational Roots Theorem the same way for .
Roots to test for, using synthetic division, are plus and minus 1/2, 1/3, 1/4, 1/6, maybe 1/12.
The negatives of those are not roots, but still you should expect up to five complex roots, since h(x) is degree 5.
(More work is necessary to find them).
(Graphing tool indicates ONE negative real root approximately  ).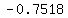
|
|
|
