SOLUTION: What is the smallest of three consecutive positive numbers if the product of the first and third is one less than eight times the second?

Algebra ->  Problems-with-consecutive-odd-even-integers -> SOLUTION: What is the smallest of three consecutive positive numbers if the product of the first and third is one less than eight times the second?      Log On


   

Question 973229: What is the smallest of three consecutive positive numbers if the product of the first and third is one less than eight times the second?
Answer by crystal5213(2) About Me  (Show Source):
You can put this solution on YOUR website!
The smallest number is equal to 7.
Explanation:
For this problem, I'll be using variables to represent the numbers: x, y, and z. But since they are consecutive, y=x+1, and z=x+2, so the numbers can be written as x, x+1, and x+2.
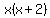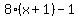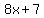According to the problem, the product of the first and third number (x%28x%2B2%29 or x%5E2%2B2x) is equal to one less than eight times the second number (8%28x%2B1%29-1%29 or 8x%2B7)
We can set the problem up like this:
x%5E2%2B2x=8x%2B7
Now we can solve it like an algebraic equation instead of a word problem. Start by moving the variable to one side of the equation by subtracting 8x from both sides, resulting in:
x%5E2-6x=7
Since there is a variable squared, we should use the quadratic formula. So we will have to subtract 7 as well, so that 0 will be on one side of the equal sign.
x%5E2-6x-7=0
According to the quadratic equation, if Ax%5E2%2BBx%2BC=0%2C then x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+
Now, we plug in the numbers.
x+=+%286+%2B-+sqrt%28+%28-6%29%5E2-4%2A1%2A%28-7%29+%29%29%2F%282%2A1%29+
in this case, a equals one because there is no number before x%5E2, so the coefficient must be 1. b is -6 since that is the coefficient for x, and c is -7.
Finally, after using a calculator to solve the equation, we get
x=7