If an arithmetic mean and a geometric mean are inserted between a and b, such
that the arithmetic mean is double the geometric mean. show that ratio of a and
b is [2+(3)^(1/2)]/[2-(3)^(1/2)]
We change the  powers to square roots
powers to square roots
 Then we rationalize the denominator:
Then we rationalize the denominator:
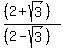

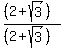
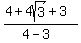

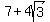


>>...the arithmetic mean is double the geometric mean...<<
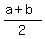

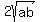 Multiply both sides by 2 to clear the fraction:
Multiply both sides by 2 to clear the fraction:
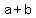

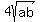 Square both sides:
Square both sides:


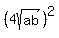


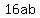
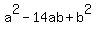


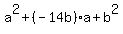

 Solve for "a" using the quadratic formula. We will use capital
letters in the quadratic formula to avoid conflict of notation:
Solve for "a" using the quadratic formula. We will use capital
letters in the quadratic formula to avoid conflict of notation:


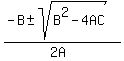 where
where  ,
,  ,
, 





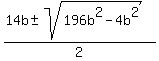


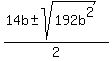


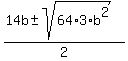


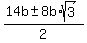


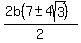


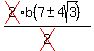


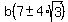 Divide both sides by b
Divide both sides by b


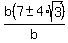





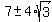 We have shown that the ratio is either
We have shown that the ratio is either 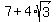 or
or 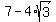 .
So you might point out to your teacher that the problem as it is stated here,
is not necessarily true.
The problem should be stated this way:
.
So you might point out to your teacher that the problem as it is stated here,
is not necessarily true.
The problem should be stated this way:
If an arithmetic mean and a geometric mean are inserted between a and b, such
that the arithmetic mean is double the geometric mean. show that ratio of a and
b is [2+(3)^(1/2)]/[2-(3)^(1/2)] OR [2-(3)^(1/2)]/[2+(3)^(1/2)].
The second one, when the  powers are changed to square roots and its
denominator is rationalized, becomes
powers are changed to square roots and its
denominator is rationalized, becomes 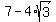 .
Edwin
.
Edwin