Question 972923: Hello Tutor, I really need your help to answer this question.
How are polar coordinates useful for working with complex numbers (hint: think about powers and roots)?
Found 2 solutions by Alan3354, KMST:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Calculating the nth power or the nth root of a complex number in the rectangular form is a complicated, messy business.
Calculate powers and roots of complex numbers in polar form is simple:
For a power: 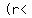   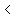 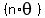 and and
for an nth root: 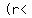   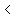  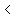 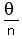
Transforming between polar and rectangular coordinates is also simple,
so if you are given the rectangular form and need to calculate a power or root,
you can easily transform to polar form, and then calculate the desired power or root in polar form.
If the result must be expressed in rectangular form, you just transform your polar form result to rectangular form.
If you have a complex number 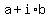 , or , or 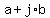 (whichever letter you use for (whichever letter you use for 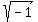 ), ),
with real part  , and imaginary part , and imaginary part  , ,
you can calculate the argument,  and modulus and modulus  from from
 and and  . .
If you know the argument,  and modulus and modulus  of a complex number, of a complex number,
you can calculate its real part  , and imaginary part , and imaginary part  as as
 and and 
|
|
|