Question 972914: 1. Adjacent sides of parallelogram are 7cm and 9cm. Its 1 diagonal is 8cm. Find its other diagonal.
2. Diagonals of parallelogram are 12cm and 26cm. One of its side is 17cm. Find the other side.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. Adjacent sides of parallelogram are 7cm and 9cm. Its 1 diagonal is 8cm. Find its other diagonal.
Two adjacent sides and that diagonal form a triangle,
with the angle between those two sides opposite that diagonal.
The law of cosines says that for a triangle with vertices A, B, and C,
opposite sides a, b, and c respectively,
the measures of angles and sides are related by
 . .
There is a triangle formed by
two sides measuring  cm and cm and  cm flanking angle cm flanking angle 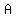 , ,
and a diagonal measuring  cm, connected to both of those sides. cm, connected to both of those sides.
That triangle, with sides so similar in length, must be an acute triangle.
Applying law of cosines to that triangle, we write




 . .
The cosine is positive, meaning that 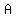 is an acute angle. is an acute angle.
In fact,  , but we do not need to calculate that. , but we do not need to calculate that.
The parallelogram looks like this:

The other diagonal  is opposite the other angle of the parallelogram, the angle at D, is opposite the other angle of the parallelogram, the angle at D,
which is supplementary to angle A, so that  , ,
and is also flanked by sides measuring 7cm and 9cm.
Those sides and the other diagonal form another triangle.

Applying law of cosines to that other triangle, we write
 ---> --->
The other diagonal measures  . .
2. Diagonals of parallelogram are 12cm and 26cm. One of its side is 17cm.Yhe  = length of the other side in cm. = length of the other side in cm.
Since the diagonals of a parallelogram bisect each other,
the longer diagonal will be split into two congruent segments,
each one measuring  , ,
and the shorter diagonal will be split into two congruent segments,
each one measuring  . .
Then, the parallelogram, divided into two pairs of congruent triangles, will look like this:

The law of cosines says that for a triangle with vertices A, B, and C,
opposite sides a, b, and c respectively,
the measures of angles and sides are related by
 . .
To find  , we can apply law of cosines to the left side triangle and write , we can apply law of cosines to the left side triangle and write
 , ,
but we do not know 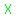 , or , or 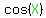 . .
However, we know that 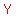 and and 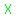 are supplementary, are supplementary,
and that because of that  . .
We can find about 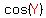 and and 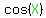 by applying law of cosines to the top triangle: by applying law of cosines to the top triangle:
 ---> ---> ---> ---> ---> ---> ---> ---> . .
Now we get back to the left triangle to find  : :
 ---> ---> ---> ---> ---> ---> ---> ---> ---> ---> ---> --->
The other side measures  . .
|
|
|