SOLUTION: Find 2 consecutive odd integers such that two -fifth of the smaller exceeds two -ninth of the greater by 4?

Algebra ->  Problems-with-consecutive-odd-even-integers -> SOLUTION: Find 2 consecutive odd integers such that two -fifth of the smaller exceeds two -ninth of the greater by 4?      Log On


   

Question 971903: Find 2 consecutive odd integers such that two -fifth of the smaller exceeds two -ninth of the greater by 4?
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!

Let x = smaller odd integer
Let x+2 = larger consecutive odd integer

two -fifth of the smaller exceeds two -ninth of the greater by 4

Replace the smaller by (x)
Replace the greater by (x+2)
We get

two -fifth of (x) exceeds two -ninth of (x+2) by 4

Recolor:


two -fifth of (x) exceeds two -ninth of (x+2) by 4

Replace two- fifth of by 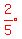red%28expr%282%2F5%29%2A%22%22%29
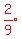Replace two- ninth of by red%28expr%282%2F9%29%2A%22%22%29

We get
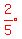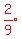red%28expr%282%2F5%29%2A%22%22%29(x) exceeds red%28expr%282%2F9%29%2A%22%22%29(x+2) by 4

Recolor:
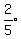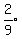expr%282%2F5%29%2A%22%22%29(x) exceeds expr%282%2F9%29%2A%22%22%29(x+2) by 4

Replace exceeds...by by =...+
We get:

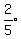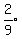expr%282%2F5%29%2A%22%22%29(x) = expr%282%2F9%29%2A%22%22%29(x+2) + 4

Multiply through by LCD = 45 to remove fractions:

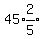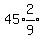45%2Aexpr%282%2F5%29%2A%22%22%29(x) = 45%2Aexpr%282%2F9%29%2A%22%22%29(x+2) + 45*4

18(x) = 10(x+2)+180

You finish:

Edwin